0 引言
无人机(unmanned aerial vehicle, UAV)执行对地作战任务具有成本低、效率高等优势, 在现代战场中应用越来越广泛。使用UAV进行进攻作战、非常规作战、高价值目标打击成为UAV发展的一个重要趋势[1]。
目前, 在UAV集群任务可靠性方面已有很多研究。一部分基于传统可靠性分析方法进行推广。文献[5-6]使用二元决策图和分阶段任务方法评估UAV集群任务可靠性; 文献[7]考虑几个自治系统执行的任务, 并提出一种通过扩展二元决策图技术来预测任务可靠性的方法; 文献[8]提出连续系统多级平衡UAV的可靠性建模和估计。还有基于概率论方法[9]、划分多级系统[10-12]、基于Agent建模与仿真系统建模[13-17]和连续时间马尔可夫链(continuous-time Markov chain, CTMC) 等建模方法[18]。此外, 用复杂网络对集群进行建模是目前一种比较热门的方法。文献[19]建立了UAV集群的多层次网络模型, 根据网络的连通性和脆弱性评估群的任务可靠性; 文献[20]用多态网络建模UAV集群, 提出考虑信息交换能力的任务可靠性评估方法; 文献[21-22]用k/n系统对UAV集群进行建模, 并基于重要性度量提出结构优化模型和数量优化模型。
上述研究成果从各个角度对UAV集群作战系统进行建模和可靠性评估。然而, 对于对地作战任务的UAV集群任务可靠性评估尚没有一套成熟的方法。在UAV集群执行对地作战任务过程中, 其任务可靠性不仅受到集群自身能力的影响, 还会受到作战环境和任务规划的影响。针对上述问题, 本文面向UAV集群对地作战过程, 定义了时态打击链(temporal operational chain, TOC)来描述UAV集群对敌方目标的攻击方式, 建立了更贴合实际作战场景的集群任务可靠性评估方法, 并且通过实例验证了该方法的合理性。
1 UAV集群时态异构作战网络模型
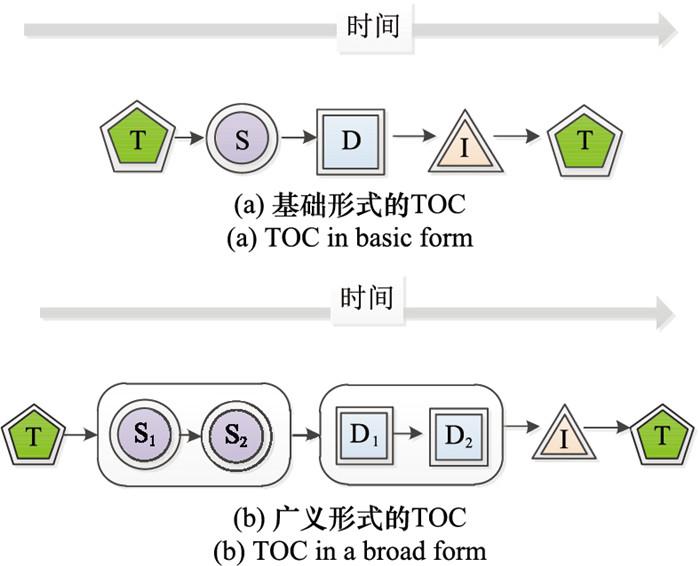
1.1 TOC的概念
表1 UAV集群异构作战网络链路分类及含义
Table 1
| 链路类型 | 含义 |
| T→S | 侦察UAV对目标实施侦察或情报搜集 |
| S→S | 侦察UAV之间进行情报信息共享 |
| S→D | 侦察UAV将探测的信息上传到决策UAV |
| D→D | 决策UAV通过信息交流进行信息共享 |
| D→I | 决策UAV向打击UAV发送打击指令 |
| I→T | 打击UAV对目标实施打击行动 |
图1
1.2 UAV群时态异构作战网络
UAV集群作战系统可以建模为异构作战网络: G=(V, E)。其中, V表示节点集, 节点集合: V=VS∪VD∪VI∪ VT, VS, VD, VI分别表示侦察UAV节点集、决策UAV节点集和打击UAV节点集, VT表示目标节点集。E表示节点之间的链路集, E=ETS∪ESS∪ESD∪EDD∪EDI∪EIT, 各链路类型的具体含义如表 1所示。
UAV集群作战过程中, UAV集群根据任务规划与敌方目标形成相应的TOC, 这些TOC相互交织, 形成一个时态作战网络(temporal combat networks, TCN)。TCN中两节点之间的联通状态可以由连接函数表示:
2 UAV生存概率模型
UAV能够执行任务的前提, 是在任务结束之前存活。而UAV在执行任务的过程中可能面临障碍物碰撞和敌方火力打击等多方威胁。有效的航路规划能帮助UAV规避一定的风险, 本文认为航路规划理论上为UAV选择了避开障碍物且满足时间限制的航路。本文主要考虑敌方防空系统(如高炮和地空导弹等)对UAV的威胁。
2.1 基于CTMC的UAV生存概率模型
相比于单架飞机而言, UAV集群中的单体UAV具有特殊性。UAV集群在执行任务时需要保持通信和一定的队形, 因此可以把UAV集群看作一个整体。其中, 每个单体UAV在执行任务的过程中可能处于5种状态: 未被探测、被探测、被跟踪、被打击和坠毁。将UAV在敌方威胁区域飞行的状态看作是UAV处于这5种状态下的随机过程, 如图 2所示。
图2
这些状态之间可能的转换取决于UAV在威胁区域的内部还是外部。当UAV进入敌方一个雷达探测区域时, 将先被探测。一段时间后, 雷达就能够对其进行稳定跟踪, 做好发射武器的准备。当UAV离开雷达探测区域后, 雷达就失去了对其进行探测, 但是因为雷达组网系统具有记忆性, 所以在一段时间内雷达仍可以预测其运动, 经过更长的时间, UAV就被完全遗忘了。当UAV进入敌方打击区域, 在敌方雷达对UAV稳定跟踪的前提下, 敌方武器系统可以启动对UAV的打击。当UAV飞离打击区域时, 敌方打击立即停止。
在t时刻从状态i到状态j的转移速率用强度λij(t)来描述。当在t时刻状态i到状态j的转移不可能发生时, λij(t)=0。马尔可夫模型与泊松过程密切相关, 其强度可以解释为转移前的预期逗留时间的倒数[28]。于是转移率矩阵Q (t)(5×5)元素可以表示为
式中: τij(t)为在t时刻从状态i到状态j转移的预期逗留时间。
2.2 状态转移前预期逗留时间的计算
UAV集群的数量会影响敌方威胁区域对单体UAV的威胁程度。一方面, UAV集群的数量越多, 整体目标越大, 单体UAV被敌方发现的概率就越大; 另一方面, UAV集群数量越多, 敌方应对单体UAV的火力被分散, 则单体UAV被打击的概率就会下降。下面分别讨论UAV在敌方雷达区域和打击区域内, 状态转移前的预期逗留时间。
2.2.1 雷达探测区域
UAV集群进入雷达探测区域后, 雷达以一定的速度对覆盖区域进行扫描, 每隔t12将覆盖区域扫描一周, 每次扫描有一定的概率扫描到目标。雷达发现目标后, 经过一段时间τ23可以形成稳定追踪。
雷达对目标的瞬时探测概率采用单元平均恒虚警处理模型计算[29], 雷达对目标的瞬时探测概率, 由目标的雷达散射截面(radar cross section, RCS)和目标与雷达之间的距离决定。其对RCS为σ0, 距离为R0的目标探测信噪比为S0, 则其对RCS为σ, 距离为R的目标探测信噪比S为
雷达对目标的探测概率为
式中: αCA为恒虚警处理常数; N为参考单元个数; Pfa为虚警概率;SNR为信噪比。
雷达探测到UAV集群的时间服从离散分布:
在同一雷达探测区域, UAV集群与雷达的距离取UAV集群在该雷达范围内的平均距离。则发现探测到UAV集群时间的分布可以简化为几何分布, 且预计探测时间:
当UAV集群离开敌方探测区域后, 预计经过τ32时间, 敌方雷达失去对UAV集群的稳定跟踪, 再经过τ21, 敌方雷达丢失UAV集群。
2.2.2 打击区域
UAV集群进入敌方打击区域后, 若敌方雷达已形成稳定跟踪, 经过τ34的武器准备时间就可以对UAV集群进行打击。假设敌人打击时目标的选择是随机的, 则每个UAV在第i顺序第被打击的概率是相同的, 都是1/n, 每次打击UAV的毁伤概率为Ph, 则第i架被打击的UAV预计毁伤时间为
所以, 每架UAV的毁伤期望时间:
式中: t45为武器单发间隔时间。
2.3 UAV生存概率计算
实际敌方的雷达探测或火力打击区域通常会有重叠。假设不同雷达或不同火力之间相互独立地探测或打击, 一个被多雷达或火力所覆盖区域的状态转移速率, 表示为所有覆盖该区域的雷达或火力区域的转移速率之和:
综上, UAV集群在同一雷达和火力区域上飞行时, 转移速率矩阵相同, 在路线穿过雷达或火力区域边界的时间点上发生变化。生存模型的转移速率矩阵可以写成分段常数矩阵:
设pTMT(tn)是描述生存模型状态概率的向量, 对于路线上的时间点tn, pTMT(tn)递归计算为
单体UAV在时间t的生存概率:
3 UAV集群任务可靠性评估
作战指挥中心通过任务分配为每个目标Ti分配了执行该任务的UAV子群Gi=ViS∪ViD∪ViI。这些UAV子群在相同的时间段内不相交, 每个子群Gi与其目标Ti在执行任务期间组成一些TOC。UAV集群任务可靠性取决于这些TOC的连通状态和作战能力。
3.1 TOC的作战能力
3.1.1 连通TOC的作战能力
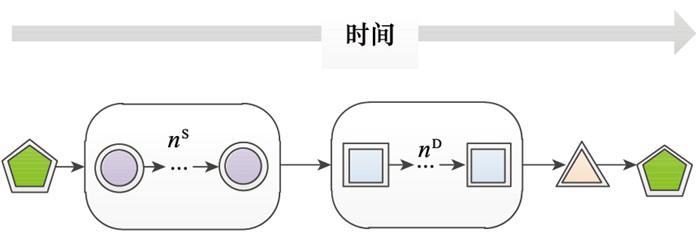
对于某个连通的TOC: lk, 构成lk的UAV集Qk=QkS∪ QkD∪{VkI}, 其中侦察UAV数量为nS, 决策UAV数量为nD。lk的作战能力可以表示如下:
式中: CS, CD, CI分别为lk在该时刻的侦察能力、决策能力和打击能力。
lk在该时刻的侦察能力CS, 即lk包含的侦察UAV集QkS的协同侦察能力表示如下:
式中: pS为单体侦察UAV的任务能力。
同理, lk在该时刻的决策能力CD, 即lk包含的决策UAV集QkD的协同决策能力表示如下:
式中: pD为单体决策UAV的任务能力。
lk在该时刻的打击能力CI, 即打击UAV: VIk所携带的武器对目标的摧毁能力pI。
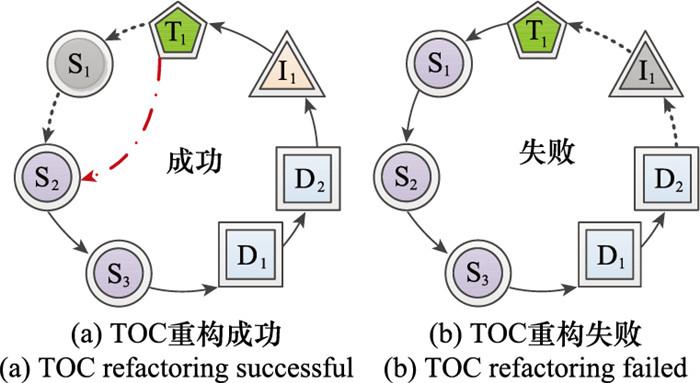
3.1.2 TOC重构过程
UAV集群在受到攻击后可能出现某些UAV坠毁, 导致所在TOC失效的情况。而UAV集群具有一定的恢复能力, 可以进行链路重构。TOC内的UAV能够相互通信, 具备链路重构的前提, 所以考虑链路内的恢复情况, 如图 3所示。当某个UAV坠毁导致链路断裂时, 如果还有同类型替代UAV, 则链路两端的节点重连。如果没有同类型替代UAV, 则该TOC失败。
图3
3.1.3 考虑链路重构的TOC作战能力
因为UAV在执行任务的过程中面临坠毁的风险, 所以实际TOC的作战能力还要考虑TOC的连通状态。如果UAV坠毁导致TOC断裂, 还要考虑TOC的重构。
TOC断裂后能够进行重构并且继续执行任务的前提是, 分别至少有一个正常运行的侦察UAV、决策UAV和打击UAV来构成TOC的基本形式。所以满足上述TOC能够通过链路重构的条件是: 正常运行的侦察UAV数量i和正常运行的决策UAV数量j都不少于1个并且打击UAV正常运行。
正常运行的UAV通过重构组成新的TOC, 有i(i=1, 2, …, nS)架侦察UAV和j(j=1, 2, …, nD)架决策UAV正常运行时, 新TOC的作战能力Uij, 根据连通TOC的作战能力的计算方法可得
设单架UAV生存概率为pl, 则有i架侦察UAV和j架决策UAV正常运行并且打击UAV正常运行的概率Pij为
因此, 考虑重构的TOC作战能力计算如下:
3.2 UAV集群执行任务可靠性
对于单个目标, 对应执行该任务的UAV子群有一组TOC: L(v)={lk}, k=1, 2, …, m用于打击该目标, 这意味着具有m种手段摧毁目标, 所以该子群对目标的打击能力可以表示如下:
式中: U(lk)是打击链的作战能力。当UAV集群的作战能力大于任务需求时, UAV集群能够完成任务, 故可靠度最高为1。
设UAV集群总共需要打击M个目标, UAV集群总的任务可靠度为
式中: ai是子目标i的重要度, ai∈[0, 1], 且满足
4 仿真分析
4.1 想定背景
图4
表2 不同集群数量下的火力分配
Table 2
| 目标 | 总编队数量 | |||
| 2 | 3 | 4 | 5 | |
| T1 | 1 | 2 | 2 | 3 |
| T2 | 1 | 1 | 2 | 2 |
| T3 | 1 | 1 | 2 | 2 |
| T4 | 1 | 2 | 2 | 3 |
| T5 | 1 | 2 | 2 | 3 |
作战场景设置如图 5所示, 任务区域中分布圆形的威胁区域, 其中包括2个雷达探测区域, 中心坐标分别为(28, 35)和(35, 55);还有4个火力打击区域, 中心坐标分别为(28, 35), (35, 55), (40, 50), (55, 60)。任务区域中散布着5个任务目标(T1~T5), 目标的重要度都设为0.2, 其坐标依次为(28, 35), (35, 55), (40, 50), (55, 60), (60, 52)。在此作战场景下, 本节为UAV集群设置了两种任务路线: 一种是集体行动的单航路任务路线, 如图 5(a)所示, 另一种是集群分开行动的双航路任务路线, 如图 5(b)所示。所规划的航路连接各目标, 目标以外的航路转弯点的坐标已在图 5上标出。UAV集群沿规划航路前往任务区域, 依次打击航路上的目标,其他各参数设置如表 3所示。
图5
表3 仿真参数
Table 3
| 装备 | 参数 | 取值 |
| 雷达区域 | 目标RCS σ0/m2 | 5 |
| 目标探测距离R0/km | 20 | |
| 目标探测概率Pd0 | 0.9 | |
| 探测虚警概率Pfa0 | 10-6 | |
| 恒虚警处理参考单元数N | 16 | |
| 搜索循环时间ts/s | 5 | |
| 预计形成追踪时间τ23/s | 10 | |
| 失去追踪时间τ32/s | 5 | |
| 遗忘时间τ21/s | 10 | |
| 火力区域 | 最大射程Rh/km | 10 |
| 武器准备时间τ34/s | 5 | |
| 单发毁伤概率Ph | 0.6 | |
| 发射间隔时间th/s | 5 | |
| UAV | 巡航速度/(km/s) | 0.2 |
| 巡航高度/km | 9 | |
| 平均RCS σa/m2 | 1 | |
| 单机侦察能力ps | 0.1 | |
| 单机决策能力pd | 0.3 | |
| 单机打击能力pI | 0.2 |
4.2 UAV生存概率仿真
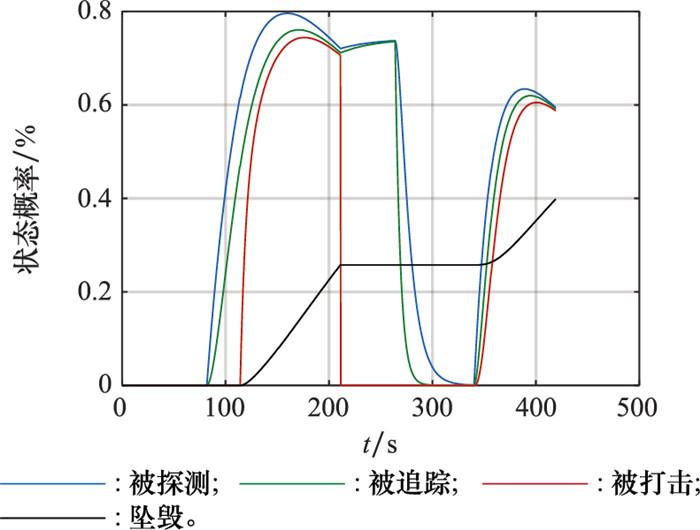
在上述任务场景下, 设置UAV集群数量n=36。模拟UAV集群按照航路2飞行时, 单体UAV状态概率随时间的变化, 仿真结果如图 6所示。UAV集群在进入第一个雷达探测区域后, 被检测、跟踪的状态概率开始增加。进入到打击区域后, 被打击和坠毁的状态概率开始增加, 坠毁概率增加也使得被检测、跟踪和打击的状态概率减小。当集群离开打击区域时, 被打击的状态概率立刻降为0, 坠毁状态不再增加, UAV仍处于敌方探测区域, 所以探测识别概率继续增加。当集群离开探测区域时, 由于雷达具有记忆性, 所以被探测和识别的概率不会立刻变为0, 而是慢慢变小, 最终雷达失去对UAV的跟踪。此后, 集群同时进入新的探测和打击区域, 被识别、被跟踪、被打击和坠毁的状态概率依次开始增加。
图6
图6
集群按照航路2飞行时UAV的状态概率
Fig.6
Probability of the state of the UAV when the swarm flies according to route 2
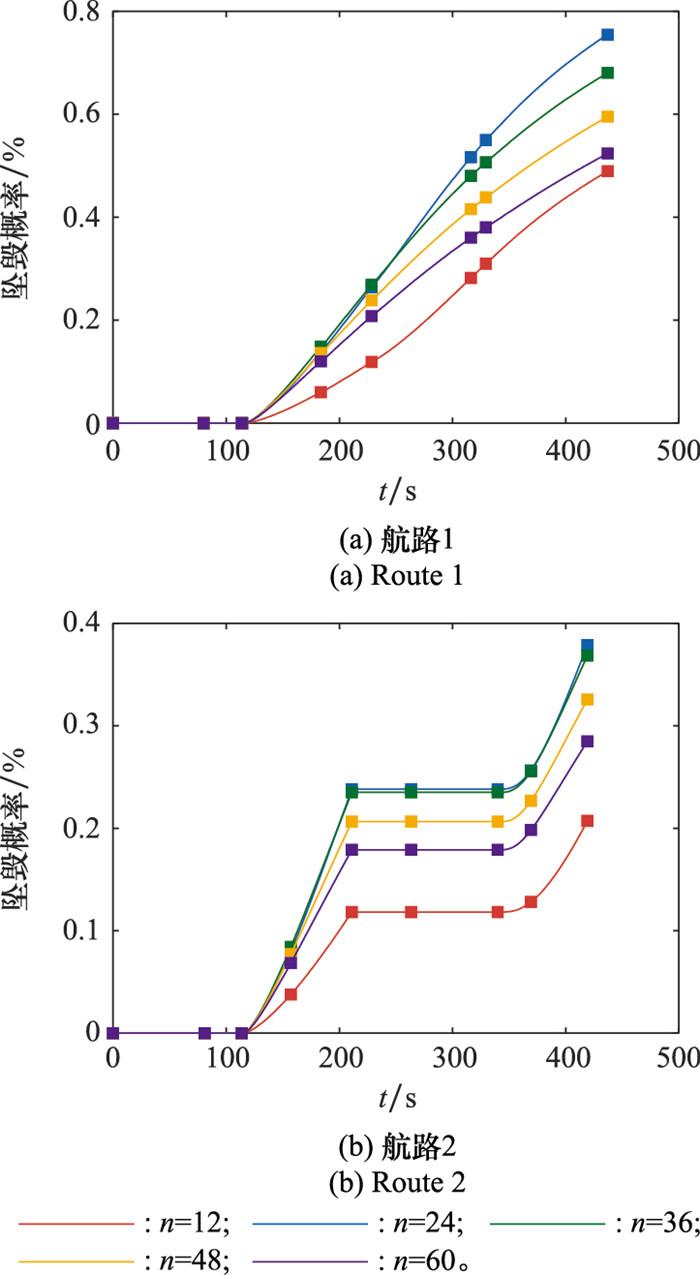
为分析集群数量变化和航路规划对单体UAV生存概率的影响, 让集群分别按照航路1和航路2飞行, 并设置不同的集群数量进行仿真, UAV的坠毁概率变化如图 7所示。由仿真结果可以看出, UAV集群沿航路1飞行比沿航路2飞行的单机坠毁概率普遍要高。这是因为沿航路1所经过的威胁区域多, 沿航路2经过的威胁区域较少且中间穿插着无威胁航段, 使得被跟踪的UAV被敌方雷达遗忘。并且不管走航路1还是航路2, 单机的坠毁概率随着集群数量增多先上升后下降。这是因为集群数量未达到一定量时, 敌方打击能力足以应付UAV集群, 集群数量对敌方对单体UAV的打击能力的影响不大。而集群数量增多会使得单体UAV的被探测概率升高, UAV被探测又是坠毁的前提, 因此集群数量增加会使得坠毁概率上升。当集群数量进一步增大, 由于敌方武器打击能力有限, 集群数量增多分散了敌方武器对单机的打击强度, 使得单机被打击的概率下降, 故单机的坠毁概率下降。
图7
图7
集群数量对单体UAV坠毁概率的影响
Fig.7
Effect of the number of swarms on the crash probability of a single UAV
4.3 集群任务可靠性仿真
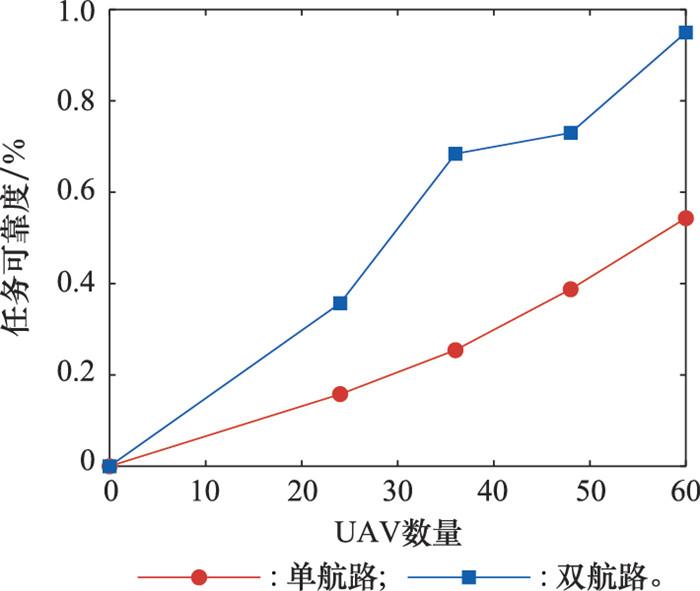
在完成UAV集群生存状态仿真的基础上, 对不同任务路线以及不同编队组成形式下的任务可靠度进行对比。先设定UAV集群按照(5 ∶2 ∶5)形式编队, 比较集群分别走单航路任务路线和双航路任务路线执行任务的可靠度。设置不同集群数量进行仿真, 仿真结果如图 8所示。
图8
再设定UAV集群走双航路的任务路线, 比较集群按照(5 ∶2 ∶5)、(6 ∶2 ∶4)和(4 ∶3 ∶5)形式编队的任务可靠度。设置不同集群数量进行仿真, 仿真结果如图 9所示。
图9
图9
编队组成形式对任务可靠度的影响
Fig.9
Effect of formation composition on mission reliability
由仿真结果可知, 单航路执行任务的可靠度明显低于双航路的任务可靠度。这是因为单航路UAV集群经过的威胁区域多, 导致UAV的生存概率小, 从而降低了任务可靠度。说明任务路线会影响任务的可靠度, 多方向突围避免UAV集群长时间暴露在威胁区域。并且还可以看出, 不管是单航路还是双航路, 集群任务的可靠度都随着集群数量的增多而升高。这说明增加UAV数量能够提升集群TCN的作战能力, 从而提高集群任务的可靠度。
由仿真结果可知, 在3种编队组成形式下, UAV集群的任务可靠度都随着集群数量的增多而升高, 统一编队数量下, 采用不同编队形式的任务可靠度也不同。这是因为不同类型的UAV单体的任务能力不同, 并且不同的编队形式导致UAV集群和目标之间形成不同的TCN, 尽管集群数量相同, 其作战能力有差异, 所以任务可靠性也有差异。说明编队组成和TCN的组成方式会影响任务的可靠度。
5 结论
本文建立了UAV集群面向对地作战过程的任务可靠性评估模型, 该模型基于UAV集群的异构特性和UAV集群执行任务过程的时态性, 考虑了敌方威胁和集群任务规划, 适用于具体任务作战情景。经过仿真验证, 该模型符合UAV集群作战规律, 具有合理性; 可以用来比较在特定任务环境下, 不同任务规划方案和UAV性能对UAV集群任务可靠性的影响, 为作战任务规划提供了参考。
参考文献
对地攻击型UAV作战效能评估
[J].
Evaluation of combat effectiveness of ground attack UAV
[J].
Multi-UAV formation control based on a novel back-stepping approach
[J].DOI:10.1109/TVT.2020.2964847 [本文引用: 1]
Ultra-reliable IoT communications with UAVs: a swarm use case
[J].DOI:10.1109/MCOM.2018.1800161 [本文引用: 1]
Generic, scalable and decentralized fault detection for robot swarms
[J].DOI:10.1371/journal.pone.0182058 [本文引用: 1]
Fast mission reliability prediction for unmanned aerial vehicles
[J].
A reliability analysis method using binary decision diagrams in phased mission planning
[J].DOI:10.1243/1748006XJRR202 [本文引用: 1]
Multiplatform phased mission reliability modelling for mission planning
[J].DOI:10.1243/1748006XJRR204 [本文引用: 1]
Reliability of balanced multi-level unmanned aerial vehicles
[J].DOI:10.1016/j.cor.2019.01.013 [本文引用: 1]
Probability modeling of autonomous unmanned combat aerial vehicles(UCAVs)
[J].DOI:10.5711/morj.11.4.5 [本文引用: 1]
Formation and adjustment of manned/unmanned combat aerial vehicle cooperative engagement system
[J].DOI:10.21629/JSEE.2018.04.10 [本文引用: 1]
MAV/UAV task coalition phased-formation method
[J].
Intervention decision-making in MAV/UAV cooperative engagement based on human factors engineering
[J].DOI:10.21629/JSEE.2018.03.10 [本文引用: 1]
Evaluating the agility of adaptive command and control networks from a cyber complex adaptive systems perspective
[J].DOI:10.1177/1548512915592517 [本文引用: 1]
基于Agent建模的机载激光武器系统作战效能影响因素分析
[J].
Analysis of the factors influencing the combat effectiveness of airborne laser weapon system based on agent modeling
[J].
Evaluating the agility of adaptive command and control networks from a cyber complex adaptive systems perspective
[J].
An evaluation method of combat aircraft contribution effectiveness based on mission success space design
[J].
基于ABMS的对地攻击型UAV体系贡献率评估
[J].
System-of-systems contribution evaluation of ground-attack UCAV based on ABMS
[J].
UAV集群作战中连续时间Markov链模型的求解方法
[J].
Solution to continuous time Markov chain model for unmanned aerial vehicle swarm operation
[J].
Unmanned aerial vehicle swarm mission reliability modeling and evaluation met-hod oriented to systematic and networked mission
[J].DOI:10.1016/j.cja.2020.02.026 [本文引用: 1]
A multistate network approach for reliability evaluation of unmanned swarms by considering information exchange capacity
[J].
Mission reliability modeling of UAV swarm and its structure optimization based on importance measure
[J].
Importance measure-based phased mission reliability and UAV number optimization for swarm
[J].
Evaluation of capability of weapon system of systems based on multi-scenario
[J].
Capability oriented equipment contribution analysis in temporal combat networks
[J].
Cognitive situation and threat assessments of ground battlespaces
[J].
Estimation of a matrix of intensities for model of Markov process
[J].