协同目标分配, 决定了兵力运用的科学性和合理性, 是将作战意图落地为作战行动的关键环节^[1]。在同一时间或空间范围内, 多个作战单元为完成同一项作战任务或相互之间存在逻辑关系的多个作战任务时, 需从时间、空间和效果等角度考虑, 进行目标或火力的合理分配, 以最大作战效费比和最小作战风险获得最优打击效果。

协同目标分配是一种典型的非线性多项式完全问题, 决策空间随问题规模(即作战单元数目和作战目标数目)增大呈指数级增长, 求解结果的的实时性、准确性和有效性将直接影响军事对抗中能否取得最佳作战效果。在军事运筹领域, 协同目标分配通常被规约为兵力分配、火力分配或武器目标分配(weapon target assignment, WTA)等问题^[2-3], 常用求解方法可分为传统规划方法^[4]、模拟退火(simulated annealing, SA)算法^[5-6]、蚁群优化(ant colony optimization, ACO)算法^[7]、粒子群优化(partical swarm optimization, PSO)算法^[8-11]、进化算法(evolutionary algorithm, EA)^[12-15]和合同网协议(contract net protocol, CNP)^[16]。现有研究虽从不同角度对各种算法进行了改进, 并成功应用于不同场景, 但关于动态不确定环境下的协同目标分配研究较少, 且难以保证大规模目标分配问题的求解效率。

在分布式作战自同步理论中^[17], 协同关系体现为作战单元“自底向上组织复杂战争的行为”。将作战单元构建为智能体, 协同目标分配问题便转化为多智能体协作(multi-agent cooperation, MAC)问题, 多智能体强化学习(multi-agent reinforcement learning, MARL)^[18]在解决类似协作问题上有着广泛应用^[19-23]。据此, 通过分析协同目标分配的军事内涵, 构建了基于MARL的协同目标分配模型, 采用局部策略评分和集中式策略推理, 利用Advantage Actor-Critic算法进行策略学习, 以期能够实现简单场景中训练好的模型直接泛化应用到复杂场景, 从而有效实现大规模目标分配。

为在统一语义框架下描述协同目标分配问题, 定义以下相关概念。

作战单元, 指能够独立遂行作战任务的基本作战单位, 为执行作战任务提供作战资源。在协同目标分配中, 作战单元是不可再分割的基本作战单位或作战平台。

作战目标, 指战场上存在且具有一定军事价值的客观实体, 是作战单元执行作战任务时所作用的客观对象。

作战协同关系, 指多个作战单元在同一时空范围内执行同一作战任务或具有逻辑关系的不同作战任务时, 在空间部署、时间衔接、目标分配、火力分配和效果达成等方面, 所形成的相互照应、相互配合和优劣互补的关系。

协同目标分配描述过程中, 定义以下符号。

(1) Tg={tg₁, tg₂, …, tgN}: 打击目标清单列表, N为打击目标总数。

(2) U={u₁, u₂, …, u_M}: 进攻方可用作战单元列表, M为作战单元总数。

(3) W={w₁, w₂, …, w_L}: 进攻方可用弹药类型列表, L为弹药类型总数。

(4) Vtg={vtg₁, vtg₂, …, vtg_N}: 各作战目标被摧毁后的收益价值列表。vtg_i为打击目标tg_i被摧毁后的收益价值, i∈{1, 2, …, N}。

(5) Vu={vu₁, vu₂, …, vu_M}: 各作战单元被摧毁后的损失价值列表。vu_j为作战单元u_j被摧毁后的损失价值, j∈{1, 2, …, M}。

(6) Vw={vw₁, vw₂, …, vw_L}: 各类型弹药消耗单位数量后的损失价值列表。vw_l为w_l类型弹药消耗单位数量后的损失价值, l∈{1, 2, …, L}。

(7) Tgl_t=(tgl_{t, 1}, tgl_{t, 2}, …, tgl_{t, N}): 执行第t次分配方案时被摧毁目标清单。tgl_{t, i}表示目标tg_i是否被摧毁, tgl_{t, i}=1表示被摧毁, 否则tgl_{t, i}=0。

(8) Ul_t=(ul_{t, 1}, ul_{t, 2}, …, ul_{t, M}): 执行第t次目标分配方案时被摧毁单元清单。ul_{t, j}表示单元u_j是否被摧毁, ul_{t, j}=1表示被摧毁, 否则ul_{t, j}=0。

(9) Wl_t=(wl_{t, 1}, wl_{t, 2}, …, wl_{t, L}): 执行第t次目标分配方案时进攻方的弹药消耗清单。wl_{t, l}表示w_l类型弹药的消耗数量。

(10) Vlsum_t: 执行第t次目标分配方案时防守方的弹药消耗价值总量。

(11) Wu_{t, j}=(w_{t, j, 1}, w_{t, j, 2}, …, w_{t, j, L}): 执行第t次目标分配方案时进攻方作战单元u_j的挂载。w_{j, l}为作战单元u_j挂载的w_l类型弹药的数目。

(12) RPro=[rpro_{l, i}]^L×N: 进攻方各类弹药对不同作战目标的命中毁伤概率矩阵。rpro_{l, i}为w_l类型弹药对作战目标tg_i的命中毁伤概率。

(13) BPro=(bpro₁, bpro₂, …, bpro_M): 防守方一体化联合防空反导对进攻方各作战单元的综合命中毁伤概率矩阵。bpro_j为对作战单元u_j的综合命中毁伤概率。

考虑使命任务、弹目匹配以及作战效费比等因素建立数学模型, 如下所示：

$\max \left[\alpha \cdot F_{1}(\boldsymbol{X})+\beta \cdot\left(\frac{F_{2}(\boldsymbol{X})}{F_{3}(\boldsymbol{X})}\right)\right]$

(1)$\text { s. t. }\left\{ \begin{array}{l}(\varPhi(t): \left\{\boldsymbol{X}_t, {\bf{BPro}}, {\bf{RPro}} \right\} \\~~~~ \rightarrow\left\{\mathrm{Ul}_t, \mathrm{Tgl}_t, \mathrm{Wl}_t, \mathrm{Vlsum}_t\right\} \\\sum\limits_{i=1}^N x_{i, j, t} \leqslant 1\\ \sum\limits_{j=1}^M x_{i, j, t} \leqslant M_i^{\prime} \\x_{i, j, t} \leqslant 1-\sum\limits_{t^{\prime}=1}^t \operatorname{tgl}_{t^{\prime}, i}\\x_{i, j, t} \leqslant 1-\sum\limits_{t^{\prime}=1}^t \mathrm{ul}_{t^{\prime}, j} \\x_{i, j, t} \leqslant f\left(\sum\limits_{l=1}^L w_{t, j, l}\right) \\i \in\{1, 2, \cdots, N\} \\j \in\{1, 2, \cdots, M\} \\l \in\{1, 2, \cdots, L\} \\t \in\{1, 2, \cdots, T\}\end{array} \right.$

(1) 模型变量

令变量x_{i, j, t}表示在第t次作战目标分配时, 是否指派作战单元u_j打击作战目标tg_i。当指派单元u_j打击目标tg_i时, x_{i, j, t}=1, 否则x_{i, j, t}=0。因此, 模型变量为

(2)$\boldsymbol{X}=\left[x_{i, j, t}\right]^{N \times M \times T}$

式中: T为作战过程中进行目标分配的总次数; 模型变量规模为N×M×T, 在相同问题背景下, 随着决策次数T的增大呈线性增长。

(2) 目标函数

模型目标函数, 衡量了作战效果的大小。参数α和β, 用于平衡两部分计算结果对目标函数值的影响；F₁(X)表示任务使命完成度, 计算方法如下所示：

$F_{1}(\boldsymbol{X})=\frac{\mathrm{Rle}-\mathrm{Ble}}{\mathrm{Rle}+\mathrm{Ble}}$

(3)$\begin{gathered}\text { s.t. }\left\{\begin{array}{r}\mathrm{Rle}=\frac{M-\sum\limits_{t=1}^{T} \sum\limits_{j=1}^{M} \mathrm{ul}_{t, j}}{M} \\\text { Ble }=\frac{N-\sum\limits_{t=1}^{T} \sum\limits_{i=1}^{N} \operatorname{tgl}_{t, i}}{N}\end{array}\right.\end{gathered}$

式中: Rle和Ble分别表示作战结束后作战单元和作战目标的剩余率。

F₂(X)/F₃(X)表示作战效费比; F₂(X)表示作战过程中摧毁敌方作战目标和消耗敌方弹药所产生的总收益; F₃(X)表示作战过程中自身作战单元被摧毁和弹药消耗所产生的总损失, 计算方法如下所示：

(4)$\begin{gathered}F_{2}(\boldsymbol{X})=\sum\limits_{t=1}^{T}\left(\sum\limits_{i=1}^{N} \operatorname{tgl}_{t, i} \cdot \mathrm{vtg}_{i}+\mathrm{Vlsum}_{t}\right) \\F_{3}(\boldsymbol{X})=\sum\limits_{t=1}^{T}\left(\sum\limits_{j=1}^{M} \mathrm{ul}_{t, j} \cdot \mathrm{vu}_{j}+\sum\limits_{l=1}^{L} \mathrm{wl}_{t, l} \cdot \mathrm{vw}_{l}\right)\end{gathered}$

(3) 约束条件

1) Φ(t)表示执行第t次目标分配方案所产生的结果。根据各方弹目匹配关系及命中毁伤概率(BPro与RPro), 执行作战目标分配方案X_t, 得到进攻方作战单元损失情况Ul_t和弹药消耗情况Wl_t、敌方作战目标被摧毁情况Tgl_t和弹药消耗总价值Vlsum_t。

2) $\sum_{i=1}^{N} x_{i, j, t} \leqslant 1$, 表示在第t次分配方案中, 作战单元u_j最多只能攻击一个作战目标。

3) $\sum_{j=1}^{M} x_{i, j, t} \leqslant M_{i}^{\prime}$, 表示在第t次分配方案中, 为避免作战资源浪费, 最多只能指派M′_i(M′_i≤M)个作战单元去攻击作战目标tg_i。

4) $x_{i, j, t} \leqslant 1-\sum_{t^{\prime}=1}^{t} \operatorname{tgl}_{t^{\prime}, i}$, 表示如果作战目标tg_i已被摧毁, 那么在以后作战目标分配方案制定中, 不再指派作战单元对其进行攻击。

5) $x_{i, j, t} \leqslant 1-\sum_{t^{\prime}=1}^{t} \mathrm{ul}_{t^{\prime}, j}$, 表示如果作战单元u_j已被摧毁, 那么在以后作战目标分配方案制定中, 不再指派该作战单元执行打击任务。

6) $x_{i, j, t} \leqslant f\left(\sum_{l=1}^{L} w_{t, j, l}\right)$, 表示若作战单元u_j已消耗完自身弹药, 那么在以后作战目标分配方案制定中, 不再指派该作战单元执行打击任务。函数$f\left(\sum_{l=1}^{L} w_{t, j, l}\right)$的计算方法, 如下所示：

(5)$f\left(\sum\limits_{l=1}^{L} w_{t, j, l}\right)=\left\{\begin{array}{l}1, \sum\limits_{l=1}^{L} w_{t, j, l}>0 \\0, \sum\limits_{l=1}^{L} w_{t, j, l}=0\end{array}\right.$

MAC问题的联合状态动作空间, 随着智能体与任务数目的增多呈指数级增长。大规模作战场景下的协同策略训练, 对训练时间和计算能力具有更高要求。因此, 如何能够实现简单场景中训练好的模型直接泛化应用到复杂场景, 是有效解决大规模协同目标分配问题的关键。诸多学者针对上述类似问题, 或利用空间近邻性构建奖励函数和任务分配策略以期实现可泛化应用模型^[24-25], 或使用集中式评价方法以期解决分散策略学习问题^[26-27]。而Carion提出了一种学习预测模型及训练方法^[28], 为解决本文问题提供了很好的借鉴。

协同目标分配, 可表示为MDP(S₁, S₂, A, R, P, m, n, π), m和n分别表示作战单元和作战目标的数目; S₁是所有作战目标的联合状态空间, S₁ⁱ(i∈{1, 2, …, m})是第i个作战目标的状态集; S₂和A是所有作战单元的联合状态空间和联合动作空间, S₂^j和A^j(j∈{1, 2, …, n})是第j个作战单元的状态集和动作集; R: S₁×S₂×A→ R为奖励函数; P: S₁×S₂×A×S₁×S₂→[0, 1]为状态转移概率; π: S₁×S₂→A为一个确定的联合策略。

考虑远期决策对当前收益影响的衰减, 动作价值函数如下所示：

(6)$q_{\pi}\left(\boldsymbol{S}_{t}, \boldsymbol{A}_{t}\right)=\mathrm{E}\left(R_{t+1}+\gamma q_{\pi}\left(\boldsymbol{S}_{t+1}, \boldsymbol{A}_{t+1}\right) \mid \boldsymbol{S}_{t}, \boldsymbol{A}_{t}\right)$

式中: S_t为时刻t作战单元和作战目标的联合状态; E(·)为求解期望值的函数。

问题目标是通过学习获取一个最优协同目标分配策略, 保证所有作战单元的协同打击行动能够使奖励函数在长期内达到最大化, 如下所示：

(7)$\pi^{*}=\arg \max \limits_{\pi} q_{\pi}$

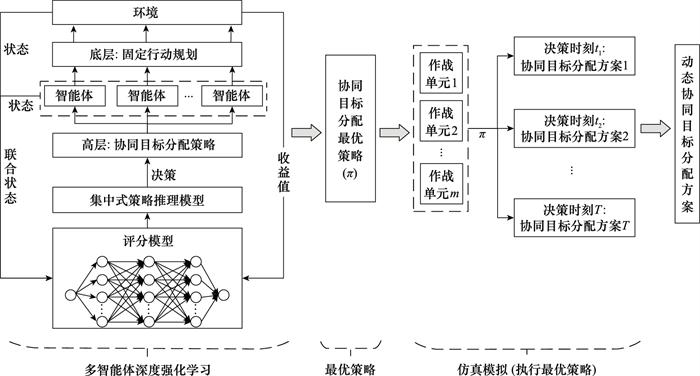
在此, 构建基于MARL的协同目标分配模型训练及应用框架, 如图 1所示, 具体流程如下。

步骤1  基于深度强化学习优化协同目标分配策略。在此, “智能体”是进攻方的各作战单元, “动作”是作战单元选择打击哪个作战目标, “环境”是本文实验平台-计算机兵棋推演系统的模拟仿真环境, “状态”为所有作战单元和作战目标的联合状态。在每一步学习中, 采用“集中式策略推理模型”获取目标分配方案, 各作战单元根据分配方案和固定行动规则对作战目标进行打击, 兵棋系统会实时返回各棋子状态和交战结果。而后, 依据系统环境返回的收益值信息, 利用基于多层神经网络的“评分模型”对该步目标分配方案进行优劣评价, 评价值用于优化策略。

步骤2  最优协同目标分配策略的模拟执行。在利用计算机兵棋系统对某次联合火力打击进行模拟仿真时, 每隔一段时间Δt, 依据最优协同目标分配策略生成目标分配方案, 各作战单元依据当前方案实时调整打击对象。当完成打击任务后, 将得到一个随时间变化的“作战目标分配方案序列”。

作战单元在各目标分配方案中分配得到的作战目标, 组成了该作战单元的打击目标序列; 作战目标在各目标分配方案中是否被打击, 形成了不同作战目标之间的先后打击顺序。

在决策时刻t, 一个确定的策略π会根据所有作战单元和作战目标的联合状态〈S_{1, t}, S_{2, t}〉, 给出能够获取最大回报的联合动作A_t=max π(S_{1, t}, S_{2, t}, t)。A_t实质就是时刻t的协同目标分配方案, 可用分配矩阵B_t等价表示, 如下所示：

(8)$\boldsymbol{B}_{t}=\left[\begin{array}{cccc}b_{1, 1} & b_{1, 2} & \cdots & b_{1, m} \\b_{2, 1} & b_{2, 2} & \cdots & b_{2, m} \\\vdots & \vdots & \ddots & \vdots \\b_{n, 1} & b_{n, 2} & \cdots & b_{n, m}\end{array}\right]$

式中: b_{i, j}表示作战单元u_j是否打击作战目标tg_i, 如果打击则b_{i, j}=1, 否则b_{i, j}=0。

若每隔时间Δt生成一次作战目标分配方案, 当完成打击任务后, 将会得到该作战场景下的一个作战目标分配方案序列, 如下所示：

(9)$\boldsymbol{B}=\left[\boldsymbol{B}_1, \boldsymbol{B}_2, \cdots, \boldsymbol{B}_t, \cdots, \boldsymbol{B}_T\right]$

当给定分配矩阵B_t后, 各作战单元将会按照固定行动规则对指派的作战目标进行打击。作战单元的行动规则包括: 作战单元自动规划打击目标的最短路径; 作战目标进入射程范围后, 作战单元将根据自身挂载的命中毁伤概率, 计算弹药发射数量; 作战单元消耗完自身弹药或油料后将自动退出作战。上述行动规划均由计算机兵棋系统自动完成, 符合军事规范并在长期应用中得到验证。因此, 学习任务将聚焦于分配策略π的学习, 而作战单元对作战目标的具体打击行为不需要进行训练。

根据协同目标分配模型的目标函数, 构建强化学习的单步奖励函数, 计算方法如下所示:

(10)$\begin{gathered}R_t=\left\{\begin{array}{l}100\left(\frac{\mathrm{bls}_t}{\mathrm{bvs}}-\frac{\mathrm{rls}_t}{\mathrm{rvs}}\right), d=0 \\r_{-} d, d=1\end{array}\right. \\r_{-} d=\left\{\begin{array}{l}100(1+\mathrm{Rle}), \mathrm{Ble}=0 ; \mathrm{Rle} \neq 0 \\-50, \mathrm{Ble}=0 ; \mathrm{Rle}=0 \\50 \frac{\mathrm{Rle}-\mathrm{Ble}}{\mathrm{Rle}+\mathrm{Ble}}, \mathrm{Ble} \neq 0 ; \mathrm{Rle} \neq 0 \\-100(1+\mathrm{Ble}), \mathrm{Ble} \neq 0 ; \mathrm{Rle}=0\end{array}\right.\end{gathered}$

式中: R_t表示在第t步得到的单步奖励值; bvs和bls_t表示防守方作战目标及弹药的总价值与第t步时被摧毁/消耗后的总收益; rvs和rls_t表示进攻方作战单元及弹药的总价值与第t步时被摧毁/消耗后的总损失; d标识作战过程是否结束, 若结束则d=1, 否则d=0;r_d为作战结束时的奖励值; Rle和Ble分别表示作战过程结束后作战单元和作战目标的剩余率。

评分模型根据作战单元和作战目标的状态，评价当前策略的优劣。在此，采用多层神经网络构建局部评分模型，通过不断学习优化模型参数来提高模型评分的精确度，可用h(s_{1, i}, s_{2, j}, θ₁)和g(s_{1, i}, s_{1, k}, θ₂)表示。其中，h(·)对作战单元与作战目标的分配关系进行评分, 反映了指派作战单元u_j打击作战目标tg_i的优劣; g(·)对作战目标之间的打击顺序进行评分, 反映了作战目标tg_i与tg_k先后打击顺序的优劣; s_{2, j}表示作战单元u_j的状态; s_{1, i}和s_{1, k}分别表示作战目标tg_i与tg_k的状态; θ₁和θ₂分别为两个神经网络的参数。

在某一决策时刻, 经过评分后可得到两个评分矩阵H和G, 分别如下所示:

(11)$\begin{array}{l}\boldsymbol{H}=\left[\begin{array}{cccc}h_{\theta_{1}}(1,1) & h_{\theta_{1}}(2,1) & \cdots & h_{\theta_{1}}(m, 1) \\h_{\theta_{1}}(1,2) & h_{\theta_{1}}(2,2) & \cdots & h_{\theta_{1}}(m, 2) \\\vdots & \vdots & \ddots & \vdots \\h_{\theta_{1}}(1, n) & h_{\theta_{1}}(2, n) & \cdots & h_{\theta_{1}}(m, n)\end{array}\right]\end{array}$

(12)$\begin{array}{l}\boldsymbol{G}=\left[\begin{array}{cccc}g_{\theta_{2}}(1,1) & g_{\theta_{2}}(2,1) & \cdots & g_{\theta_{2}}(n, 1) \\g_{\theta_{2}}(1,2) & g_{\theta_{2}}(2,2) & \cdots & g_{\theta_{2}}(n, 2) \\\vdots & \vdots & \ddots & \vdots \\g_{\theta_{2}}(1, n) & g_{\theta_{2}}(2, n) & \cdots & g_{\theta_{2}}(n, n)\end{array}\right]\end{array}$

式中: h_θ1(i, j)表示对作战单元u_j打击作战目标tg_i的评分; g_θ2(i, k)表示对作战目标tg_i与tg_k打击顺序的评分。

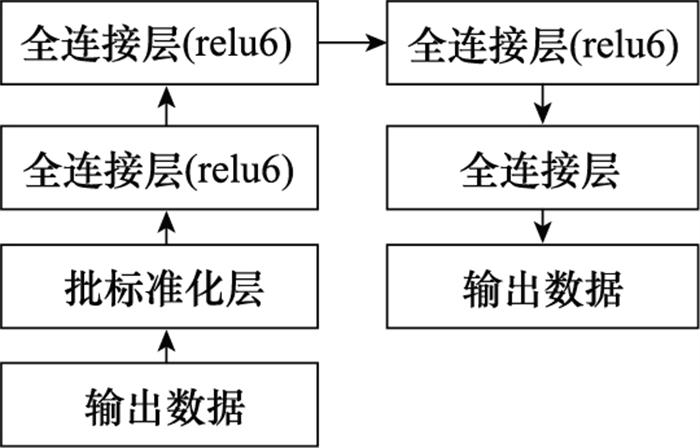
评分模型h(·)和g(·)分别采用结构相同但参数不同的神经网络, 如图 2所示。h(·)的输入数据为评分对象“作战单元和作战目标”的联合状态向量; g(·)的输入数据为评分对象“作战目标和作战目标”的联合状态向量。作战单元和作战目标的特征状态, 包括类型、位置、自身价值、弹药携带量和弹药单位价值。输入数据经过批标准化层和4个全连接层后, 输出评分数值。

协同策略推理模型主要负责根据评分矩阵H和G确定能够获取最大评分总数的分配矩阵B_t。在协同目标分配策略π为确定性策略时, 分配矩阵B_t只与当前t时刻各作战单元和作战目标的联合状态有关。在学习过程中, 分配矩阵B_t还取决于评分模型的网络参数θ₁和θ₂。因此, 可使用参数化B_t(S₁, S₂, θ₁, θ₂)表示分配矩阵。

一种贪婪的策略推理, 是将作战单元指派给h(·)分数最高的作战目标。但贪婪地选择分数最大的作战单元打击作战目标, 实质是默认打击目标的效益与指派打击该目标的作战单元数目呈正比例关系。然而, 当作战单元和作战目标数目较多时, 打击某一作战目标的总收益, 会随着指派作战单元的数目增大而趋于饱和, 从而导致严重的资源浪费。因此, 需要限制打击同一作战目标的作战单元数量。

此外, 还需要考虑不同作战目标的先后打击顺序。当考虑作战目标之间的约束关系时, 可能会出现两种极端情况: 一种情况是作战目标之间的相关关系较弱, 则作战单元会被“分散”指派给各个作战目标并同时执行打击任务; 另一种情况是作战目标之间存在较强的相关关系, 则作战单元会被“集中”指派去打击重要性较大的作战目标, 而后按照重要性顺序依次打击其他作战目标。在实际作战中, 作战目标之间的重要性对比关系, 应处于上述两种极端情况之间。

协同策略推理过程, 可表示为

(13)$\begin{aligned}\max \sum\limits_{i \in n, j \in m} b_{i, j} h\left(i, j, \theta_{1}\right)+\sum\limits_{i, k \in n ; j, l \in m} b_{i, j} b_{k, l} g\left(i, k, \theta_{2}\right) \\\text { s.t. }\left\{\begin{array}{l}\sum\limits_{i=1}^{n} b_{i, j} \leqslant 1 \\\sum\limits_{j=1}^{m} \phi_{i, j}\left(s_{i}, s_{j}\right) b_{i, j} \leqslant \phi_{i}\left(s_{i}\right) \\b_{i, j} \in\{0, 1\} \\\phi_{i}\left(s_{i}\right) \in \bf{R} \\\phi_{i, j}\left(s_{i}, s_{j}\right) \in \bf{R} \\i, k \in\{1, 2, \cdots, n\} \\j, l \in\{1, 2, \cdots, m\}\end{array}\right.\end{aligned}$

式中, b_{i, j}为分配矩阵B_t(S₁, S₂, θ₁, θ₂)中第i行第j列的元素, 表示作战单元u_j是否打击作战目标tg_i; h(i, j, θ₁) 为评分矩阵H中第i行第j列的元素, 表示指派作战单元u_j打击作战目标tg_i的优劣程度; g(i, k, θ₂)为评分矩阵G中第i行第k列的元素, 表示对作战目标tg_i与tg_k的打击顺序的评分; 约束条件$\sum b_{i, j} \leqslant 1 $, 表示指派作战单元u_j打击的作战目标数目最多为1; ϕ_i(s_i)表示打击作战目标tg_i的最大弹药需求量, 使用ϕ_{i, j}(s_i, s_j)表示作战单元u_j打击作战目标tg_i的打击效果; 约束条件$\sum \phi_{i, j}\left(s_{i}, s_{j}\right) b_{i, j} \leqslant \phi_{i}\left(s_{i}\right)$表示指派打击作战目标tg_i的作战单元的打击效果之和不能超出该作战目标的打击需求。

协同目标分配策略的优化, 需要通过学习算法实现。在此, 将“评分”视为一个负责顶层决策的虚拟中心智能体的“动作”, 将“评分模型”作为需要学习的“策略”, 将协同策略推理过程和仿真模拟环境统一看作为学习“环境”, 通过A2C (advantage actor-critic)算法^[29-30]进行策略优化。策略网络Actor用于逼近“评分模型”, 评价网络Critic用于逼近整个“环境”运行产生的累计回报。学习优化的基本过程, 如图 3所示, 具体步骤如下。

步骤1  策略网络Actor为第2.2节中所构建的评分模型。神经网络接收当前作战单元和作战目标的空间分布状态, 通过网络前向传播计算评分矩阵H和G。然后, 将H和G作为“动作”输出给协同策略推理模型。

步骤2  协同策略推理模型根据评分矩阵H和G, 通过策略推理制定协同目标分配方案, 具体方法如第2.3节所述。然后, 将协同目标分配方案下达给各作战单元, 各作战单元按照底层固定的行动策略执行目标打击任务。

步骤3  评价网络Critic接收目标分配方案单步执行后产生的奖励值, 单步奖励值的计算方法如式(11)所示。然后, 通过神经网络的前向传播计算执行“动作”H和G所产生的评价值, 并更新优化网络参数。最后, 将计算得到的关于收益的TD-error输出给策略网络Actor。

步骤4  策略网络Actor接收TD-error后, 更新优化评分模型的网络参数θ₁和θ₂。

步骤5  迭代上述过程, 直至学习结束。

在某型计算机兵棋系统上, 以联合火力打击为例, 验证本文协同目标分配方法。

(1) 实验设计与数据

实验背景: 为保证联合任务部队能够顺利渡海登陆, 现对敌沿岸雷达阵地、防空阵地、机场和指挥所进行联合火力打击。

实验思路: 构建两个不同复杂度的实验场景, 如表 1所示; 在小场景中进行模型训练, 而后在相同场景下, 应用训练好的模型进行仿真模拟, 验证模型构建和训练的合理性; 最后, 将训练好的模型直接泛化应用的大场景中, 验证解决大规模问题的有效性。实验数据: 敌我双方武器平台、作战目标及弹药的价值系数, 是综合造价和影响己方作战程度而计算的评价值。敌方一体化防空反导, 弹药类型以W表示, 其价值系数为0.05。综合考虑武器平台性能及挂载类型、作战目标性质以及弹目匹配关系, 敌我双方的“武器-目标”命中毁伤概率, 如表 2所示。

(2) 小场景下模型训练与验证

由于“武器-目标”命中毁伤概率小于1, 即便训练得到的策略最优, 也会出现收益值很差的情况。在此, 将每一轮训练的总回报, 设置为本次训练总回报与前一轮训练总回报的综合值, 计算方法如下所示:

(14)$G_{n+1}^{\prime}=0.9 G_n^{\prime}+0.1 G_{n+1}$

式中: G′_n+1为第n+1次训练周期的综合回报值; G′_n为第n次训练周期的综合回报值; G_n+1为第n+1次训练周期的原始回报值。

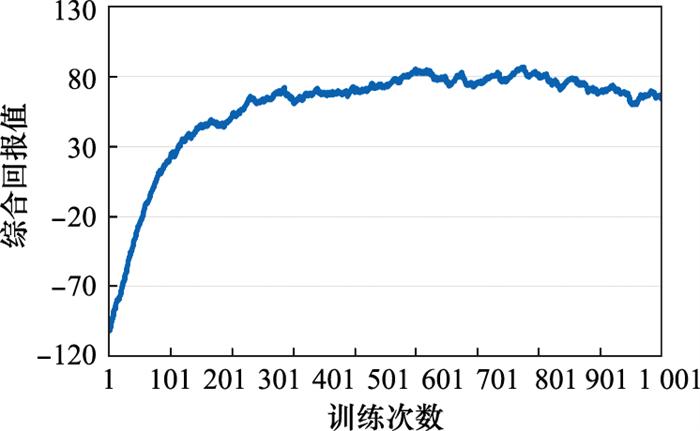
根据本文方法构建评分模型、推理模型和学习模型, 利用计算机兵棋系统进行1 050轮学习训练。训练过程中, 综合回报值随训练次数的变化曲线, 如图 4所示。可见, 基于A2C算法的策略优化方法能够保证策略回报值趋于收敛, 从而得到最优协同目标分配策略。

在相同场景下, 使用训练好的模型和策略, 进行70次模拟仿真验证, 统计以下信息: 模拟仿真回报值, 如图 5(a)所示; 任务完成度(作战目标的摧毁数目与初始数目之比)和进攻方作战单元剩余率, 如图 5(b)所示。

(3) 大场景下模型泛化应用

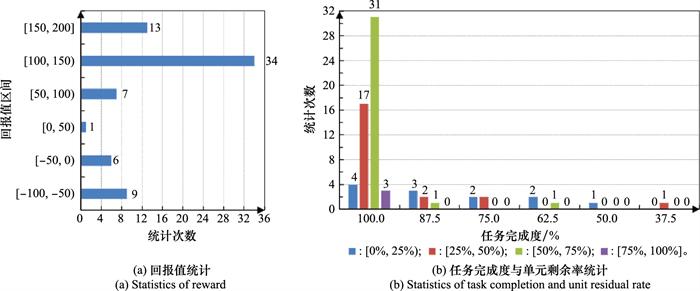
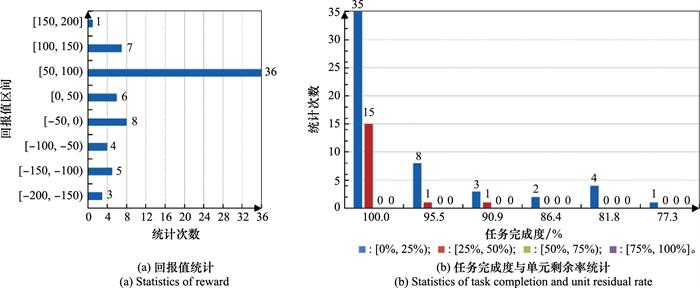
在大场景下, 不进行任何学习训练, 直接使用小场景中训练好的模型和策略, 进行70次模拟仿真泛化应用验证, 统计信息如图 6所示。

(4) 实验结果分析

1) 在小场景验证实验中, 综合回报值落在区间[50, 200]的模拟次数占总次数的77%;能够百分之百完成打击任务的模拟次数占总次数的78.6%, 而能够保证自身损失不超过50%的模拟次数占总次数的48.6%。虽然存在我方损失很大而敌方损失较小的情况, 但非协同分配策略导致, 而是由于敌我双方命中毁伤概率小于1产生的小概率随机结果。因此, 训练优化的策略能够保证进攻方以较小损失完成联合火力打击任务。

2) 在大场景泛化应用实验中, 综合回报值落在区间[50, 200]的模拟次数占总次数的62.9%;能够百分之百完成打击任务的模拟次数占总次数的71.4%。相比小场景实验, 进攻方的作战单元损失较大且收益平均值较小。主要原因是大场景下作战目标是小场景的2.75倍, 而武器平台只是小场景的1.9倍, 因此进攻方会产生更大的损失。但训练优化的策略, 依旧能够保证进攻方以较大概率完成联合火力打击任务。

本文针对传统方法难以实现动态不确定环境下的大规模协同目标分配问题, 提出了基于MARL的协同目标分配方法。通过策略分层将学习任务聚焦于顶层分配策略的学习, 构建了策略评分模型和策略推理模型, 并基于A2C算法进行策略的优化学习。实验结果表明, 基于多智能体系统对作战单元协同作战行为进行建模, 能够形象地刻画协同作战的演化内因; 基于A2C算法的策略优化方法, 能够确保最优协同目标分配策略的有效生成; 而生成的最优目标分配策略, 能够在执行时以较好的效果完成联合火力打击任务。