0 引言
作为一种兼具战略威慑和战术打击能力的新型武器, 临近空间高超声速飞行器(near space hypersonic vehicle, NSHV)具有飞行高度高、飞行速度快、突防能力强、打击威胁大等特点, 通常飞行于20~100 km的临近空域[1-2], 飞行速度大于5 Ma。近年来, 以美俄为首的军事大国加大开展高超声速飞行器核心技术和攻防体系的研究, 逐步迈入工程研制阶段, 并不断有印、法、日、英等国家加入NSHV的研制行列[3-4]。可以预见, 未来几年内,NSHV技术领域的竞争将越发激烈, 各国空天安全将面临新的挑战, 对NSHV的早期预警、稳定跟踪和防御拦截成为迫切需求。因此, 为解决NSHV难以进行三维稳定跟踪的问题, 进一步对其跟踪技术及理论进行研究尤为必要。
对NSHV跟踪的问题实质上是利用最新量测信息不断对系统预测状态进行修正的过程, 主要包括两个核心内容: 机动模型和滤波算法, 其中机动模型决定了系统预测状态的发展趋势, 滤波算法用来修正系统的预测误差[5-7]。由于NSHV高机动的特性, 采用常规卡尔曼滤波在跟踪时,易发生精度下降甚至滤波发散的现象。因此, 建立符合NSHV运动特性的机动模型和设计更为鲁棒的滤波算法是提高NSHV跟踪精度、实现稳定跟踪的可行路径。在机动模型方面, 单一的经典机动模型如匀速(constant velocity, CV)模型、匀加速(constant acceleration, CA)模型、当前统计(current statistical, CS)模型、Singer模型、Jerk模型等难以进行稳定有效的跟踪[8-10], 系统预测误差较大。文献[11]以CS模型为中心, 结合CV模型, 设计了一种修正变结构交互多模型(interactive multiple model, IMM)算法, 使模型切换更为灵活。文献[12]结合NSHV目标的周期性滑跃特点, 对加速度的时间相关性进行建模, 设计了一种针对NSHV特性的跟踪算法。文献[13]分析了NSHV目标的机动特性, 将加速度建模为衰减震荡自相关的随机过程, 并分析了模型的适应性。在滤波算法方面, 以常规卡尔曼滤波算法为基础, 引入渐消因子,从而实时调整过程噪声协方差,克服滤波发散[14-16]。文献[17]分析了造成Kalman滤波发散的原因, 并对算法的一步预测值进行了修正, 提高了滤波稳定性。文献[18]对传统的衰减记忆算法进行了改进, 提出了一种可以智能衰减陈旧信息, 合理补偿当前信息的强跟踪算法, 改善了跟踪效果。考虑NSHV目标的机动特性, 单一的从机动模型或滤波算法的角度出发,实现可靠跟踪较为困难, 不能适应其复杂机动特点。
基于此, 本文首先分析了NSHV目标的机动特性, 将其三维运动轨迹分解到纵向弹道和横向弹道, 在两个弹道上分别建立适合其运动特征的跟踪模型。其次,基于量测噪声协方差和残差设定了修正门限, 引入多重渐消因子,实时调节各通道的权重, 并设计了一种限定记忆长度的指数加权新息协方差估计方法,对陈旧量测信息进行限定记忆, 提高新近量测数据的影响。最后通过仿真实验对算法进行验证。
1 目标机动特性分析与运动建模
1.1 机动特性分析
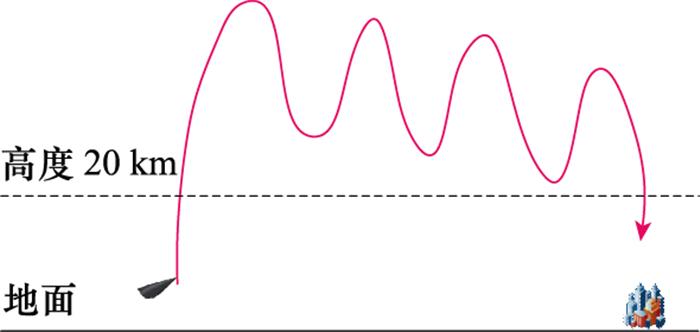
图1
攻角和倾侧角是NSHV目标的主要控制参量。其中, 攻角主要影响目标纵向弹道的机动形式, 其设定受飞行走廊的约束, 通常采用线性、常值或分段函数进行描述:
式中: L为目标所受升力; M为目标质量; υ为倾侧角; θ为速度倾角; r为地心距; g为重力加速度。
攻角取值在满足式(1)的条件下, 目标处于平衡滑翔状态, 在其他取值情况下, 目标处于跳跃滑翔状态[21]。而倾侧角对横纵向弹道都有影响, 决定了目标横向弹道的机动形式, 其设定同样受飞行走廊的约束, 主要是为了规避探测、机动突防, 可以进行类似大C或S型横向机动。倾侧角的设定主要是有利于进攻方进行打击摧毁, 受敌方实际战场环境的影响较大, 但复杂的横向机动会增大被探测的概率, 降低攻击时效。
1.2 运动学模型构建
基于上述分析, 将NSHV目标空间机动弹道分为纵向机动弹道和横向机动弹道。在纵向弹道上, 根据加速度衰减震荡特性, 将其建模为二阶时间自相关的零均值随机过程[13]; 在横向弹道上, 其加速度变化相对简单, 采用Singer模型和CA模型进行IMM滤波。最后通过并行滤波和合并处理形成完整的NSHV目标三维跟踪。
1.2.1 纵向弹道模型
根据NSHV目标纵向方向上加速度的衰减震荡特性, 将加速度建模为二阶时间相关函数[13], 即
式中:第Ⅰ部分体现了加速度的指数衰减特性;第Ⅱ部分体现了加速度的周期特性;τ为时间差;σa2为加速度方差;α为最大相关衰减量;β=2π/ΔTc为机动震荡频率;ΔTc为震荡周期。
该相关函数的功率谱密度为
式中: w为角速率。
令G(w)=[α-(β-w)j][α+(β+w)j], 则有
式中:W(wj)为白噪声的傅里叶变换。可得到加速度a(t)的微分方程为:
式中: w(t)是方差为2ασa2的零均值高斯白噪声, 其状态方程为
对式(6)进行离散化, 则其状态转移矩阵为
式中:
其过程噪声为
过程噪声协方差QDO(k)=E(W(k)WT(k)), 具体详见文献[13]。
1.2.2 横向弹道模型
在横向弹道上, 其加速度变化相对简单, 滤波器采用CA模型和Singer模型。CA模型将加速度建模为白噪声, 其离散化时间状态[5]方程为
式中:状态转移矩阵为
协方差矩阵QCT为
式中:Sw为白噪声的功率谱密度。
Singer模型由Singer在1970年提出, 将加速度建模为具有指数自相关的零均值随机过程[22], 自相关量为
加速度微分方程为
此处α为的机动时间常数的倒数, 即机动频率, 与纵向弹道运动模型中的α含义类似。其离散化时间状态方程为
式中:
其过程噪声协方差矩阵参见文献[5]。
2 基于多重渐消因子的自适应卡尔曼滤波方法
根据第1节分析可知, 跳跃滑翔NSHV目标的加速度具有震荡特性, 其机动样式相对灵活多变, 单纯采用常规卡尔曼滤波算法进行滤波易发生跟踪精度下降。因此, 本文设计了一种基于多重渐消因子的自适应卡尔曼滤波方法, 增强滤波算法的自适应跟踪能力。
设采样周期为T, 离散系统的时间状态方程和量测方程可表示为
式中: X(k)和Z(k)分别表示目标k时刻的状态向量和量测向量; F(k)表示k时刻的状态转移矩阵; H(k)表示k时刻的量测矩阵; Γ(k-1)为k时刻的系统噪声矩阵; W(k)和V(k)分别表示k时刻的状态噪声和量测噪声。
典型的离散时间卡尔曼滤波过程可表示为
在给定目标状态向量初始值和估计状态向量的协方差初始矩阵后, 滤波便可以根据最新量测信息进行持续递推。
一般而言, 造成卡尔曼滤波精度下降或发散的原因主要有3种: 一是建立的目标机动模型不准确; 二是目标运动状态发生突变; 三是滤波迭代过程中估计误差的传递[17]。对卡尔曼滤波进行修正的本质就是利用最新量测值对预测值进行修正, 减小估计误差。而当预测值偏离实际值较大时, 增大修正的比重, 防止滤波发散, 这就是传统渐消卡尔曼滤波的基本思路。但是这种修正实际上依赖量测值的准确性, 也就是当量测值本身误差非常大时, 这种修正的意义非常有限。同时, 传统渐消卡尔曼滤波的单一渐消因子在处理多通道滤波时, 对各通道的调节能力相同, 导致滤波精度降低。因此, 本文设计了一种多重渐消因子的自适应卡尔曼滤波方法, 能自适应调节各通道的过程噪声协方差权重, 并设定了发散程度判断门限, 降低量测误差的影响, 提高滤波器整体性能。
2.1 修正门限值的设定
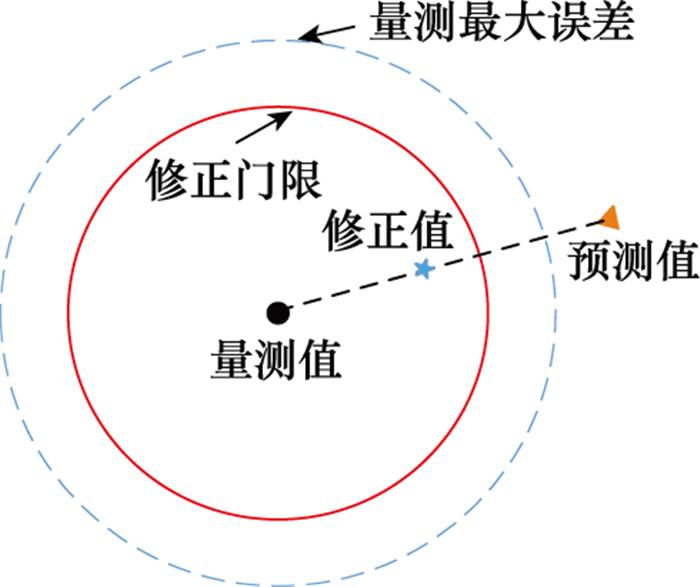
由于量测值本身是存在误差的, 为降低量测误差的影响, 保证滤波器的优良性能, 在对预测值进行修正之前设定修正门限。只有当预测值与量测值的误差大于修正门限时, 才启动多重渐消自适应滤波, 否则继续执行常规卡尔曼滤波。这里, 用r(k)衡量预测值与量测值的误差, 用量测误差协方差的均方值表示量测值最大误差, 门限设定为
图2
2.2 多重渐消因子的选取
式(21)中如果引入标量渐消因子ρ, 则可表示为
式中:ρ(k)≥1, 则标准卡尔曼滤波将变为单渐消因子卡尔曼滤波[23]。
标量渐消因子ρ的确定方法为
式中:
式中: N为滑动窗口长度。
从式(27)~式(29)可以看出, 当处理多通道滤波时, 单渐消因子ρ(k)对各通道滤波的调节能力相同。为避免这种缺陷, 本文引入多重渐消因子ρ(k), 能根据各通道的实际滤波情况对各通道进行实时调节。
式中: n为状态向量维数; ρ(i)表示第i维状态向量对应的渐消因子。
定义矩阵J(k)= Γ(k-1)P(k-1)ΓT(k-1), 则有M(k)=H(k)J(k)HT(k)。而量测矩阵H(k)中的元素通常为0或1两种取值, 故由ρ(k)M(k)=N(k), 可得出多重渐消因子的计算方式为:
式中: Hi(k)表示k时刻量测矩阵中的第i个元素。
当ρ(k)=I时, 多重渐消滤波退化为常规卡尔曼滤波。从式(32)可以分析, ρi(k)的取值受新息协方差估计值
2.3 新息序列协方差的估计
由式(29)可以看出, 经开窗法计算得到的新息协方差估计值
设限定新息协方差序列的记忆长度为N(N≤k), 加权系数为χ (i), 在时刻k应满足
式中: b为遗忘因子, 通常取值范围为0.7~0.95。确定遗忘因子b后, 根据数列性质, 有:
因此,
下面推导新息协方差的递推公式。k时刻的新息协方差估计
k-1时刻的新息协方差估计
从式(35)和式(36)可以看出, 式(35)的Ⅰ项可以用
由式(37)可得出, 新息协方差估计值的大小依赖于记忆长度N和遗忘因子b的取值, 其中N和b取值的选取主要取决于系统状态的变化剧烈程度, 对于变化越平缓的系统, 记忆长度N的取值应越大, 遗忘因子b的取值同样也应越大, 以此得到更准确的新息协方差估计值。
3 仿真实验
3.1 观测方程的建立
式中: A为方位角; E为俯仰角; rm为目标距离; λE=e-σE2/2, σE2为俯仰角误差平方, λA=e-σA2/2, σA2为方位角误差平方。量测噪声协方差R为
式中: R为对称矩阵, 修正无偏量测转换后R内各元素为
式中: λ′A=e-2σA2=λA4; λ′E=e-2σE2=λE4; σr2为测距误差平方。
3.2 仿真场景设置
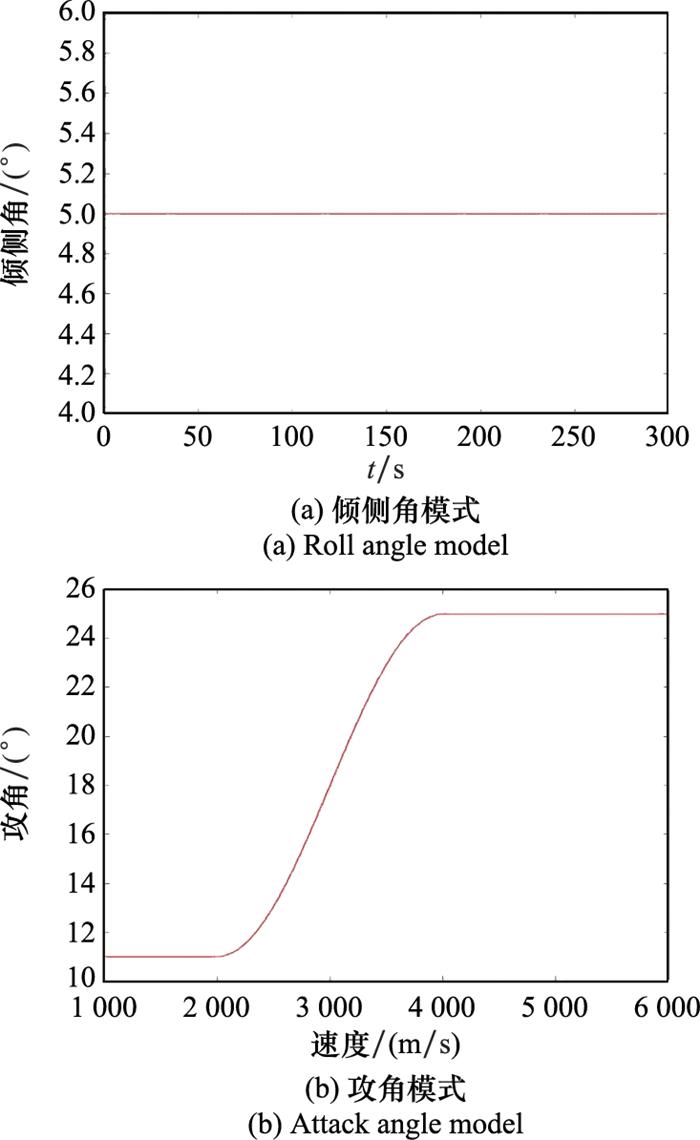
参考美国官方公布的CAV-H飞行试验, 设置如下仿真场景: 高超声速滑翔飞行器目标由发射器助推到50 km高度并释放后进行滑翔, 其再入速度为15 Ma, 攻角和倾侧角模式如图 3所示。
图3
攻角模式表达式为
式中: vmid=(v1+v2)/2;αmid=(αmax+αmax-K)/2;αbal=(αmax-αmax-K)/2;αmax=25°; αmax_K=11°; v1=4 000 m/s; v2=2 000 m/s。
假定观测雷达地理坐标为[12°, 1.5°, 1 km], 采样间隔为0.1 s, 距离误差为100 m, 俯仰角和方位角误差均为0.1°, 雷达观测过程中无地面遮挡, 目标与雷达距离约为300 km。
为验证本文算法性能, 设置两个仿真实验, 实验1主要验证本文算法相对其他算法跟踪NSHV目标时的精度, 实验2主要验证本文算法在不同量测参数下的跟踪稳定性。
3.2.1 仿真实验1
选取CA+CV+CS的IMM滤波算法、文献[12]所提的跟踪算法以及基于本文运动模型的常规卡尔曼滤波算法作为对比, 分析各模型的跟踪效果。其中, 目标在各坐标轴对应的加速度方差σa2=102, 加加速度方差
(1) CA+CV+CS的IMM滤波算法: 机动频率为1/20, 最大加速度amax=10g, 模型先验概率u0=[0.1,0.8,0.1];
(2) 文献[12]所提跟踪算法: 角速率w0=0.05;
(3) 本文运动模型: 机动震荡频率β=0.06 rad/s, 最大相关衰减量α=1/300。
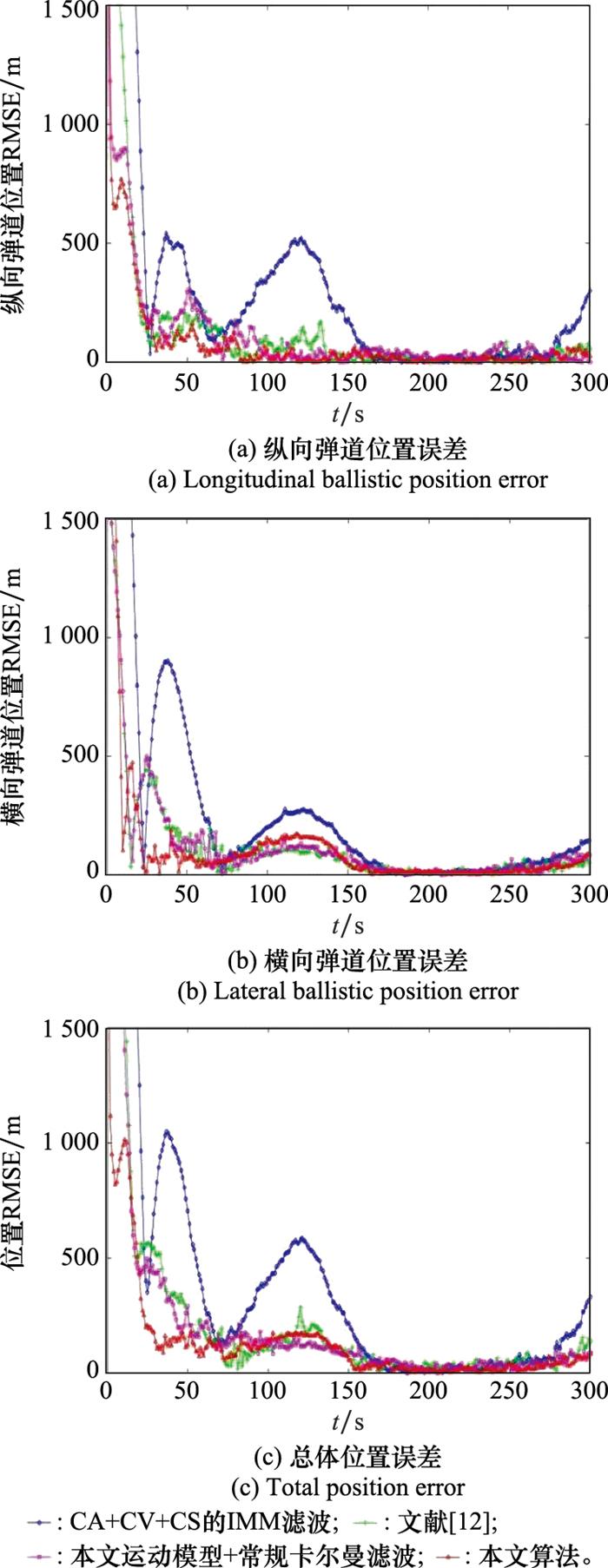
图4
图5
图6
从位置跟踪误差可以看出, 由于CA+CV+CS的IMM滤波算法对目标运动模式建模不够准确, 在50~150 s的时间区间, 其纵向和横向弹道跟踪误差都存在明显起伏, 且收敛速度较慢。文献[12]提出的跟踪算法在跟踪类周期运动目标时能保持较好的性能, 能快速收敛并保持较为稳定的跟踪效果, 没有明显剧烈的误差起伏, 但由于NSHV机动并不是严格周期性运动, 所以其总体跟踪误差较本文运动模型稍差。本文提出的运动模型能较准确地描述NSHV的运动模式, 所以其跟踪效果较好, 但由于常规卡尔曼滤波器对误差的修正有限, 所以在0~80 s的跟踪阶段, 其收敛速度要逊于本文算法。
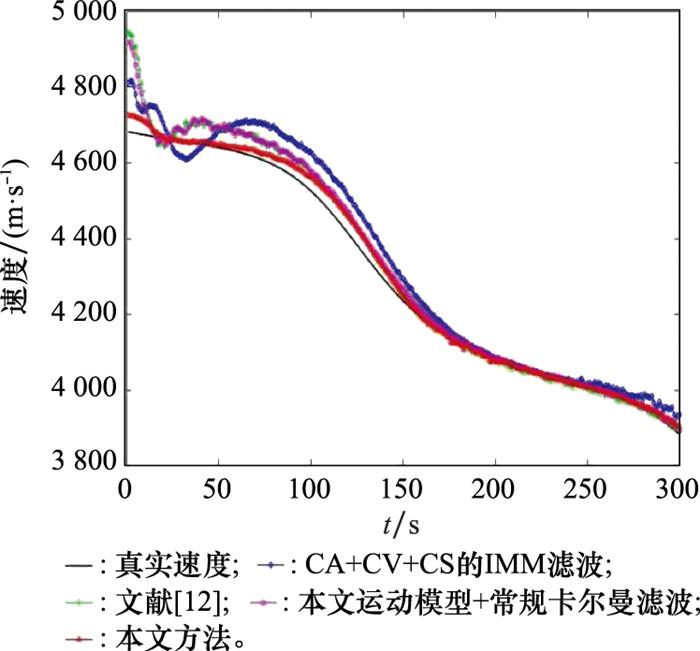
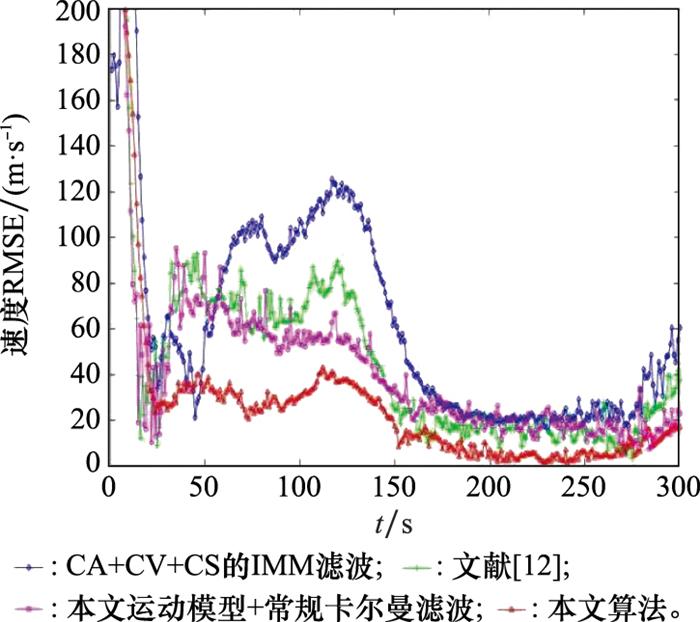
从速度误差来看, 本文算法收敛速度最快, 且整体较为平稳, 精度最高。由于NSHV目标的机动特性, CA+CV+CS的IMM滤波算法速度跟踪误差起伏最大, 其他2种算法整体差别不明显, 本文运动模型的常规卡尔曼滤波算法估计误差精度略优。
位置与速度误差统计平均如表 1所示。
表1 目标位置与速度跟踪误差统计平均
Table 1
| 算法 | 位置误差/m | 速度误差/(m·s-1) | ||
| 纵向弹道 | 横向弹道 | 总误差 | ||
| CA+CV+CS的IMM滤波 | 337 | 353 | 690 | 81 |
| 文献[10]所提算法 | 128 | 167 | 295 | 62 |
| 本文运动模型+卡尔曼滤波 | 126 | 162 | 288 | 60 |
| 本文算法 | 120 | 81 | 201 | 44 |
3.2.2 仿真实验2
为检验本文算法在不同量测参数下的跟踪性能, 在保持其他各种仿真条件不变的情况下, 设置了如表 2所示的几种不同量测参数。
经过仿真实验分析, 可得到不同滤波器参数下, 本文算法的位置和速度跟踪误差如表 3所示。
表3 不同滤波器参数下的误差比较
Table 3
| 算例 | 误差 | |
| 位置/m | 速度/(m·s-1) | |
| 1 | 201 | 44 |
| 2 | 324 | 65 |
| 3 | 367 | 73 |
| 4 | 441 | 82 |
从表 3可以看出, 量测误差协方差增大1倍后, 算法的位置估计误差和速度估计误差分别增大61%、48%, 采样周期增大1倍后, 算法的位置估计误差和速度估计误差分别增大83%、66%, 量测误差协方差和采样周期同时增大1倍后, 算法的位置估计误差和速度估计误差分别增大119%、86%。这是因为采样周期增大后, 跟踪会变得“迟钝”, 收敛速度变慢, 导致误差上升; 量测误差协方差增大后, 导致量测值对预测值修正变弱, 收敛速度变慢, 跟踪误差上升。但总体上, 本文算法在不同量测参数下保持了较为稳定的跟踪性能, 能较好适应滤波器的参数变化。
3.3 仿真结果与分析
第3.2节所述仿真实验可以表明:
(1) 对于NSHV目标的跟踪, 不同跟踪模型在其机动样式稳定时, 都能保持较小的误差并进行稳定跟踪, 但当NSHV目标机动样式发生改变时, 由于跟踪模型失配, 不能反映目标真实运动状态, CA+CV+CS的IMM滤波算法、文献[12]所提的跟踪算法、基于本文运动模型的常规卡尔曼滤波算法都会发生明显的误差上升, 而本文算法则可以根据滤波发散情况对渐消因子进行实时调整, 利用最新量测值对预测值进行修正, 所以跟踪效果要优于常规卡尔曼滤波, 且滤波收敛后依然能保持稳定的滤波性能。
(2) 由于跟踪性能的优劣与量测参数直接相关, 从仿真实验2可以看出, 本文算法在不同的量测参数下, 滤波性能有所差异, 但总体还是保持了较为稳定的跟踪, 没有发生明显的滤波发散, 说明本文算法具有一定的“抗干扰能力”, 稳定性较好。
4 结论
针对NSHV目标跳跃滑翔的机动特性, 本文将其三维运动轨迹分解到纵向弹道和横向弹道, 在两个弹道分别建立适合其运动特征的跟踪模型, 并针对常规卡尔曼滤波在跟踪误差较大时易发生精度下降的现象, 构建了多重渐消因子的自适应卡尔曼滤波, 提高了收敛速度和跟踪精度, 并与常用的几类跟踪模型进行了仿真对比, 结果表明本文算法在跟踪NSHV目标时精度和稳定性均较高。
参考文献
Cooperative space object tracking using space-based optical sensors via consensus-based filters
[J].DOI:10.1109/TAES.2016.140506 [本文引用: 1]
The advancement of lunar gravity model due to the development of space tracking techniques
[J].
Survey of maneuvering target tracking. Part Ⅰ: dynamic models
[J].
Coupled dynamic model of state estimation for hypersonic glide vehicle
[J].
高超声速滑翔目标自适应跟踪方法
[J].
An adaptive tracking method for a hypersonic glide target
[J].
Estimating optimal tracking filter performance for manned maneuvering targets
[J].
A Jerk model for tracking highly maneuvering targets
[J].
Design of an interacting multiple model algorithm for air traffic control tracking
[J].
临近空间非弹道式目标跟踪修正变结构滤波
[J].
Tracking filter for nonballistic near space targets based on MVSIMM algorithm
[J].
临近空间高超声速滑跃式机动目标的跟踪模型
[J].
A tracking model for near space hypersonic slippage leap maneuvering target
[J].
A damped oscillation model for tracking near space hypersonic gliding targets
[J].DOI:10.1109/TAES.2019.2897517 [本文引用: 4]
Robust adaptive Kalman filter for estimation of UAV dynamics in the presence of sensor/actuator faults
[J].DOI:10.1016/j.ast.2012.12.003 [本文引用: 1]
M-estimator-based robust Kalman filter for systems with process modeling errors and rank deficient measurement models
[J].
A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices
[J].DOI:10.1109/TAC.2017.2730480 [本文引用: 1]
基于修正卡尔曼滤波的目标跟踪
[J].
Target tracking based on amendatory Kalman filter
[J].
Intelligent fading memory for high maneuvering target tracking
[J].
高超声速滑翔飞行器典型弹道特性分析
[J].DOI:10.3873/j.issn.1000-1328.2015.04.005 [本文引用: 1]
Typical trajectory characteristics of hypersonic glide vehicle
[J].DOI:10.3873/j.issn.1000-1328.2015.04.005 [本文引用: 1]
Marginal tracking algorithm for hypersonic reentry gliding vehicle
[J].
临近空间高超声速跳跃式滑翔目标跟踪模型
[J].DOI:10.3969/j.issn.0372-2112.2018.09.024 [本文引用: 1]
A tracking model for near space hypersonic jumping gliding target
[J].DOI:10.3969/j.issn.0372-2112.2018.09.024 [本文引用: 1]
Highly maneuvering target tracking using multi-parameter fusion Singer model
[J].DOI:10.21629/JSEE.2017.05.03 [本文引用: 1]
基于自适应多重渐消因子卡尔曼滤波的SINS初始对准方法
[J].
SINS initial alignment method based on adaptive multiple fading factors Kalman filter
[J].
An adaptive Kalman filter based on sage windowing weights and variance components
[J].DOI:10.1017/S0373463303002248 [本文引用: 1]
一种多级助推段弹道导弹跟踪算法
[J].DOI:10.3873/j.issn.1000-1328.2016.09.011 [本文引用: 1]
A tracking algorithm of ballistic missile with multi-stage boosters
[J].DOI:10.3873/j.issn.1000-1328.2016.09.011 [本文引用: 1]