武器装备体系是指由多个功能上相互联系、相互作用的装备协同工作、有机整合而形成的新质作战力量, 以协同编队作战体系为例, 各平台分别承担态势感知、任务规划、指挥决策、行动控制、火力打击等功能, 在战争中杀伤链路可快速闭合，形成非对称优势，发挥歼击要害等重要作用。某类海上作战体系由航空母舰、濒海战斗舰、无人水面舰艇、无人机、直升机和通信链路等平台组成, 这些平台协同工作进行探测并消灭目标, 如目标船只、潜艇和鱼雷等。同时, 该体系的各组成平台都具有一个或多个能力, 并通过系统之间的协作形成更高级别的作战能力。可以说, 以数据和信息技术为代表的高新技术的广泛应用, 将国防设施与装备通过网络数据与通信系统相连接, 实现了体系要素之间的互联、互通、互操作, 使得系统或装备之间的联系和交互变得越来越频繁和紧密, 从而实现体系整体的稳定、可靠与智能化运行。

装备体系有多系统集成、维数大、可变元素多、涌现性和演化性强等特点。在任务环境下, 武器装备体系具有节点易损毁、时间强约束、任务高动态、拓扑快演化等特征, 其局部异常情况(包括节点故障、功能退化、结构拓扑失效等内部扰动, 以及任务变化、对抗干扰、环境冲击、拦截破坏等外部扰动)可能诱发体系任务链条断开、拓扑结构崩溃、信息传输中断、杀伤网络瘫痪等全局性异常或失效, 增加其整体运行的内在风险, 使体系性能发生降级, 降低任务执行效率, 甚至导致顶层任务失败。为适应战争需求, 针对体系任务受强对抗环境影响大、难以评价可靠性动态影响等问题, 开展装备体系/集群可靠性建模与预计方法研究, 对确保装备体系在跨域、捷变、强干扰等复杂作战条件下安全可靠地完成各项任务具有重要作用。

由于装备体系具有复杂性、涌现性、整体性、协同性与开放性等复杂特性, 应用当前面向复杂系统的可靠性工程方法已经无法有效地解决与处理装备体系相关问题。体系可靠性是体系战斗力生成和保持的重要基础, 不仅直接影响着装备的作战模式、作战规模以及持续作战能力, 影响效能的发挥和提高, 影响装备的全生命周期费用, 而且直接反映了体系战备完好性和完成作战任务的成功率, 对于战争进程具有重要的影响。因此, 为提升装备体系的作战能力, 亟需开展装备体系可靠性建模与预计方法研究, 为提升装备体系作战效能提供有力支持。

目前, 在装备体系可靠性研究方面尚处于初期阶段, 主要集中在概念和技术框架上, 还未形成一套完整的、可有效处理体系问题的工程化方法论。装备体系可靠性建模方法主要应用包括马尔可夫链、表决系统模型、离散事件仿真、Petri网、系统动力学和复杂网络理论等。其中, 基于复杂网络理论进行体系可靠性、脆弱性、鲁棒性和韧性的研究被广泛采用^[1-3]。杨克巍等^[4-5]以装备体系为对象, 围绕装备体系架构、体系需求工程、装备体系建模分析与仿真评估、网络体系建模分析与分析方法、体系优化设计理论与方法、体系贡献度等内容展开研究。罗爱民等^[6-7]以装备体系为对象, 围绕军事架构技术、体系结构建模、军事信息系统综合集成和装备体系分析评价等方面开展研究。潘星等^[8]基于体系工程中需求开发和能力要求分析, 提出了以装备体系保障为中心的装备体系可靠性、维修性、保障性指标与论证方法。龙慧^[9]基于复杂网络理论对武器装备网络模型优化以及风险评估进行了研究。Dui等^[10]利用表决系统和重要度理论, 提出了无人飞行器集群任务可靠性建模与拓扑结构优化设计方法。Wang等^[11]利用多层级耦合网络和复杂网络脆弱性指标, 建立了面向系统和网络化任务的无人飞行器集群任务可靠性建模与评估方法。Liang等^[12]基于秩分布-标准熵、全端可靠性和自然连通性三类指标, 对水下航行器集群任务可靠性进行多方面的分析与评估。然后, 基于复杂网络建模方法仅针对其网络拓扑特性进行建模描述, 分析集群复杂网络指标, 但复杂网络指标尚无确定的评价与衡量标准, 且对装备体系节点的异质性和连边的有向性考虑不足。

近年来, 装备体系研究重点已从随机过程、复杂网络和多智能体系统转向OODA(observation, orientation, decision, action)环和杀伤链理论^[13]。装备体系中各组成系统具有不同的功能, 如探测、识别、决策、通信和打击。当多个装备系统以体系形式运行时, 可以协同结合为OODA环。在装备体系中, OODA环是指多个装备进行迭代协调的过程, 通过交互和合作以实现共同的目标, 其强调了装备的相互关联性, 使其能够适应并有效地完成复杂任务。由于外部冲击在装备体系运行中逐渐变得不可预测和不可避免^[14], 很难评估各种外部冲击影响下的装备体系可靠性。通过考虑OODA环和杀伤链遭受木马、电磁攻击和火力攻击等外部冲击的情况, 为装备体系可靠性建模与预计提供了一个新的视角。Chen等^[15]提出了有效杀伤链概念, 并给出可重构无人装备体系任务可靠性建模与预计方法。Sun等^[16]提出了一种基于杀伤链的无人机群作战能力评估方法。Li等^[17]利用OODA环和杀伤链的概念, 建立了一种基于时间作战网络、面向能力的装备贡献分析方法。通过集成分层参考架构和杀伤链。Hahn等^[18]提出了信息物理系统的安全性分析框架。Singh等^[19]通过集成基于网络、基于模型和机器学习的入侵检测系统, 为智能电网构建了基于网络杀伤链的混合入侵检测系统框架。Li等^[13]分析了基于杀伤链的无人装备体系作战网络的结构鲁棒性, 为设计更具弹性的无人装备体系提供技术支撑。Jia等^[20]建立了基于加权超网络的搜救体系定量能力评估模型。Xu等^[21]建立了包括蜂群模型开发、失效模型、韧性评估以及级联失效和自修复机制的无人自主蜂群的失效分析框架。Liu等^[22]通过考虑不同的恶意攻击策略, 提出了一种基于复杂网络的集群可靠性评估方法。Li等^[23]利用OODA环和杀伤链, 探索了具有不同类型功能实体和信息流的异构无人装备体系功能鲁棒性。Sun等^[24]提出了基于多集群协同的无人装备体系韧性模型与评估算法。王耀祖等^[25]提出了基于杀伤链路的作战体系网络模型和关键节点识别方法。白光晗等^[26]面向集群编队队形和任务, 建立基于表决系统的无人机集群任务可靠性模型。

综上, 装备体系可靠性建模与预计方法研究仍处于初级阶段, 且多为静态可靠性模型, 未充分考虑装备体系动态变化过程中各要素、层次、状态以及结构和功能逻辑关系等因素; 基于实时对抗仿真的评估方法计算资源消耗大, 成本高, 效率低, 难以满足作战任务过程中体系可靠性预计的实时性要求, 建模的标准化程度不足, 不利于评估结果的可信性提升, 尚缺乏系统的可靠性建模与预计的理论、方法与工具支撑。因此, 本文通过考虑内外部干扰和动态重构策略, 提出了一种基于广义有效OODA环的装备体系可靠性建模与预计方法, 以指导装备体系结构设计, 确保装备体系在作战任务中能够可靠地执行任务, 从而提升其作战效能。

以网络为中心的自同步指挥控制等概念的出现, 将体系中各装备通过网络数据和通信系统连接起来, 以实现互联、互通、互操作, 成为了实现网络化、协同化作战的基础。要提高现有复杂装备体系的作战能力, 使其适应未来多变的作战任务环境, 应针对装备体系未来的作战任务需求, 结合当前装备体系发展现状, 科学地开展装备体系建设规划与总体论证。武器装备体系论证中涉及两个重要的因素: 作战效能和作战适用性。其中, 适用性主要包括: 可靠性、维修性、可用性, 安全性等特性。尽管对单一武器装备的通用质量特性论证已经积累了大量的实践经验, 形成了较为规范的论证过程和方法, 但对于武器装备体系的通用质量特性论证则还在探索中, 尤其是对于装备体系的论证过程、论证方法和技术等方面尚有欠缺。装备体系以逻辑空间为载体, 以信息空间为核心, 以数据为基础, 具有资源共享、信息融合的综合化特性。装备体系结构已从传统以“物理”为核心逐渐转变为以“事理”为核心。例如, 装备系统可靠性与装备体系可靠性设计有本质区别, 装备体系的可靠性设计需要站在体系设计的角度, 充分考虑装备体系中的各系统、网络及要素, 分析装备体系的失效机理与模式, 有针对性地制定可靠性设计准则。本文通过对装备体系通用质量特性概念辨析, 分析给出了装备系统与装备体系通用质量特性的区别与联系, 如表 1所示, 装备体系可靠性模型见本文第3.3节。

本节基于OODA环理论, 根据装备体系的拓扑结构和要素, 建立其节点和链路模型。然后, 利用异质有向图建立装备体系有效OODA环和OODA网络模型。

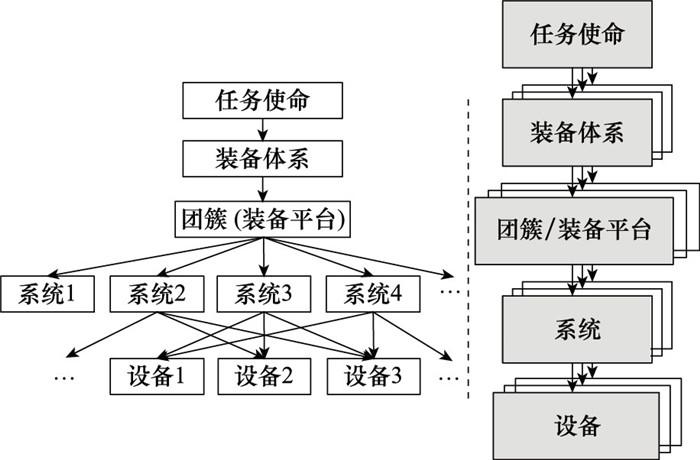
若干具有单独作战能力的团簇(无人系统团簇)或平台(驱逐舰、护卫舰等大型有人平台)通过“资源与信息共享”形成了以网络为中心的、具有协同作战能力的武器装备体系。在装备体系中, 每个团簇或平台都需要执行一组任务(目标或子目标)以实现体系的总体任务, 因此该装备体系对任务使命的实现需要解决任务分配、冲突处理、组成系统之间的协同能力等问题。装备体系中的组成系统与关键设备通过通信网络实现资源与信息的共享, 使得体系形成一个有机的整体。因此, 装备体系的形成主要是装备要素的协同。装备体系层次结构的划分能体现出体系的复杂性和涌现性等特征, 而不同的体系结构层次划分方式对体系研究的侧重点和作用也各有不同。根据各个层次的特性对整个体系属性的不同影响, 本文的装备体系结构层次划分如图 1所示。

在实际作战过程中, 装备体系中的各种军事装备及作战资源种类繁多, 基于OODA环理论, 本节将装备体系要素定义为影响装备体系核心作战能力的主要组成系统或装备。影响装备体系作战能力的组成系统或装备有很多, 对基于OODA环的装备体系要素的识别无法、也没有必要涵盖各平台系统所有的系统。因此, 在对装备体系进行分析或指标构建时, 需要简化或者忽略对装备体系影响不大的因素, 只考虑将对装备体系影响较大的系统或装备作为装备体系的关键要素。

依据装备体系结构及OODA环的概念内涵, 在武器装备设计、运行及其任务执行过程等各个阶段, 按照影响装备体系的关键能力得到影响装备体系的4个要素。

(1) 侦察探测要素

在装备体系作战任务过程中, 侦察探测系统如同装备体系的眼睛, 肩负发现敌情、识别敌情等重要职责。同时, 每个作战平台都有多台各司其职的探测系统协同工作。因此, 将侦察探测要素确定为影响装备体系作战能力的主要因素之一。

(2) 指挥控制要素

在装备体系作战任务过程中, 指挥与控制系统如同装备体系的大脑, 肩负处理敌情、下达作战指令等重要职责。装备体系的每个作战平台都配有作战指控设备, 且以其中某一指控系统为主指控系统, 负责下达所有作战指令, 其他平台指控系统则互为备份。因此, 指挥控制要素也在文中被确定为影响装备体系作战能力的主要因素之一。

(3) 武器要素

武器要素即火力系统, 如同装备体系的四肢, 肩负火力打击、防空反导等重要职责。其中, 不同作战平台装载有不同型号的武器以及独立的火控系统, 因此装备体系的各平台具有不同的火力打击能力。作为装备体系最终的执行机构, 火力要素也被确定为影响装备体系作战能力的主要因素之一。

(4) 通信要素

在装备体系执行作战任务的过程中, 通信系统如同装备体系的神经, 肩负联合组网、信息传递等重要职责。同时, 每个作战平台内部通过有线局域网和平台之间的无线数据链, 实现了装备体系内节点之间侦察探测信息、指挥控制信息、协同火控信息的实时传输和交换, 并且使装备体系实现了资源实时共享、信息实时融合、探测协同探测、武器协同控制作战。因此, 将通信要素确定为影响装备体系作战能力的主要因素之一。

装备体系要素是作战力量的主要源泉, 上述4个关键要素是实现作战活动OODA过程的基础, 其他辅助系统对装备体系效能的影响程度较低, 故本研究将侦察探测、指挥控制、武器和通信确定为装备体系要素, 并对其进行建模与分析。针对主要的作战要素, 以图论中的节点作为模型, 忽略其装备实际大小与飞行角度等因素的影响, 等效为有向图中的节点。根据装备与资源实际作战功能不同, 将装备体系节点分为侦察探测(Sensor)节点、决策(Decider)节点、火力(Weapon)节点3类。装备体系各平台的物理资源之间以信息为介质, 以网络为载体, 进行资源与信息的共享, 以实现共同的目标, 完成共同的使命, 因此通信网络是实现各物理资源之间“资源与信息共享”的前提与基础, 其功能丧失会使平台或系统节点失去协同作战能力, 本文将节点之间的通信等效为链路。团簇通常指无人系统集群(如无人机群), 本文也指代大型装备平台(如侦察机、驱逐舰和护卫舰等大型作战装备)。装备体系节点和链路类型如表 2所示。

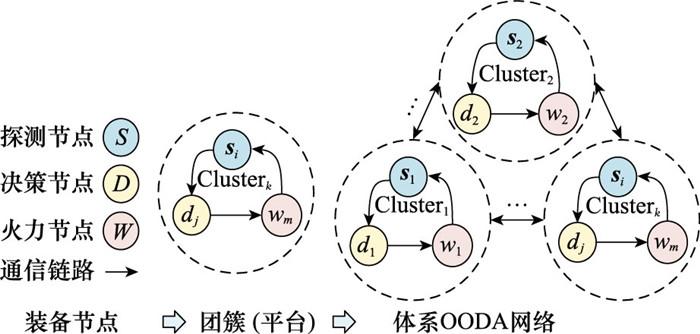
在理想状态下, 装备体系各节点可以相互连接, 形成一个全连通的网络。然而, 在实际任务场景中, 不同类型的组成系统节点会受到自身属性和运行资源的约束。本文定义s_i(i=1, 2, …, I)表示第i个探测节点, d_j(j=1, 2, …, J)表示第j个决策节点, w_m(m=1, 2, …, M)表示第m个武器节点, I, J, M表示不同类型节点的数量; e_{si, dj}和e_{dj, wm}分别表示节点s_i到d_j和d_j到w_m的关联关系。基于OODA环的武器装备体系组成结构如图 2所示。

针对节点故障建模, 首先, 装备在任务执行过程中会发生自然退化和随机失效现象。此外, 在作战任务执行过程中节点或团簇容易遭受各种类型的外部冲击和干扰, 如病毒、电磁冲击和火力打击等, 不同类型冲击对不同节点造成的损伤程度也不相同, 且会同时影响到体系中的部分节点或全部节点。同时, 同平台或团簇内的节点具有关联关系会引发共因失效。因此, 需要同时考虑节点的上述失效模式，建立节点失效模型。

随机故障以不可预测的方式发生, 导致节点从体系中被移除。考虑到装备固有的可靠性, 采用指数分布或泊松分布结合蒙特卡罗方法来准确描述其失效行为。节点s_i, d_j, w_m的故障或消亡由参数为λ_i^s, λ_j^d, λ_m^w的泊松分布来描述。节点s_i, d_j, w_m的修复或生成由参数为μ_i^s, μ_j^d, μ_m^w的指数或泊松分布描述。

蓄意攻击是指旨在对系统或其组件造成伤害或破坏的蓄意行为。这些攻击一般都有特定的目标和策略。其中, 最常见的蓄意攻击策略由Albert等^[27]于2000年提出。Hao等^[28]提出了树形攻击策略, 该攻击策略可应用于网络病毒入侵等类型的外部干扰分析。最大度攻击策略和最大介数攻击策略分别根据节点的度和介数中心性从高到低排序的节点移除策略。本文主要考虑最大度攻击策略对体系的影响, 设k_i^s, k_j^d, k_m^w表示节点s_i, d_j, w_m的度。

对于探测类S节点, 其主要是雷达、察打一体无人机等装备。由于侦查探测装备的型号不同, 其可靠性也会有较大的差距。探测节点S的模型建立为: s_i(I, λ_i^s, μ_i^s, k_i^s, cluster_k)。其中, I表示探测节点的数量; cluster_k表示节点s_i是团簇k的成员。

决策节点D主要由指挥决策系统和指挥无人机等组成。D的属性模型建立为: d_j(J, λ_j^d, μ_j^d, k_j^d, cluster_k)。其中, J表示决策节点的数量; cluster_k表示d_j是团簇k的成员。

火力节点W主要包括导弹、巡飞弹等。火力节点W的模型建立为: w_m(M, λ_m^w, μ_m^w, k_m^w, cluster_k)。其中, M表示火力节点的数量; cluster_k表示w_m是团簇k的成员。

装备体系连边代表节点之间的通信和关联关系。连边承载的信息促进了体系内节点之间的数据传输、命令和任务分配。边的存在表明其所连接的节点之间存在直接联系和交互, 其在实现体系节点之间的协调行动、协作和信息交换方面发挥着至关重要的作用, 最终提升装备体系整体作战效能。体系节点之间通过有线局域网或无线数据链连接, 节点间的通信表现为有向关系。本文将团簇内部和团簇之间的通信定义为具有不同权重的有向边, 给出基于加权有向图的装备体系连边模型。

本研究建立了一个基于OODA环的加权有向边模型:

(1) $E=\left\{e_{s_i, d_j}, e_{d_j, w_m}\right\}$

连边e_{si, dj}传输侦察任务信息, 考虑了节点s_i和d_j之间的通信距离和可靠性。e_{si, dj}模型建立如下:

(2) $e_{s_i, d_j}\left(d_{s_i, d_j}, R_{s_i, d_j}^c\right)$

式中: d_{si, dj}和R_{si, dj}^c分别为s_i和d_j的通信距离和可靠性。

连边e_{dj, wm}传输作战任务信息, 其中考虑了节点d_j和w_m之间的通信距离和可靠性。e_{dj, wm}模型建立如下:

(3) $e_{d_j, w_m}\left(d_{d_j, w_m}, R_{d_j, w_m}^c\right)$

式中: d_{dj, wm}和R_{dj, wm}^c分别为d_j和w_m的通信距离和可靠性。

装备体系的系统功能及其关联关系存在差异, 简单的同质有向网络无法有效描述不同系统之间的关系。因此, 本研究采用异质网络构建有效的OODA网络模型, 从而赋予不同节点和连边实际意义。异质有向网络定义如下。

异质有向网络: 给定一个有向图D=(V, E, φ, ψ), 该有向图有一个节点类型映射函数为φ(V)→ξ, 其中v∈V属于特定的节点类型φ(v)∈ξ。有向图D中, 每条边e_ij都表示由i到j的一对有序节点。边类型映射函数为ψ: E→ζ, 其中每条边e∈E都属于一个特定的关系ψ(e)∈ζ。如果有向图D的节点类型|ξ|>1或边类型|ζ|>1, 则该网络模型为异质网络。

在本文中, 装备体系由不同类系统组成, 其中|ξ|=3, |ζ|=2。V=(S, D, W), 其中S={s₁, s₂, …, s_I}, D={d₁, d₂, …, d_J}, W={w₁, w₂, …, w_m}; E={e_{si, dj}, e_{dj, wm}}, 其中连边e_{si, dj} ∈E意味着从s_i到d_j的信息传输。

OODA环是一种闭环结构, 在现实战场中, 装备体系通常需要多个OODA环交互耦合, 共同完成作战任务。第2节和第4节考虑内外部干扰因素对于OODA环节点与连边的影响, 并融入动态重构策略提出有效OODA环模型。一个OODA环中的节点也可能出现在其他OODA环中, 而且同类节点之间可以进行信息融合和资源共享。因此, OODA环通过共享相似节点进行协作, 从而形成如图 3所示的有效OODA网络。本文给出有效OODA网络模型定义。

有效OODA网络模型通过对传统OODA环模型进行扩展, 纳入了节点随机失效、蓄意攻击和体系动态重构等因素影响OODA环完成任务的实际效果, 装备体系中的线性OODA环交叉融合形成异质有向网络结构, 体系中的组成系统通过共享资源和整合信息来实现任务目标。有效OODA网络模型可用一个集合表示:

(4) $\text { eOODA_network }=\{\boldsymbol{A}, V, E\}$

式中: A ={A_SD, A_DW}表示不同节点之间连接的邻接矩阵集合。例如, 节点S和D的邻接矩阵如下所示:

(5) $\boldsymbol{A}_{S D}=\begin{aligned}& \begin{array}{c}& & & d_1 & & d_2 & & d_3 & & \cdots & & d_J\end{array} \\& \begin{array}{c}s_1 \\s_2 \\s_3 \\\vdots \\s_I\end{array}\left[\begin{array}{ccccc}x_{s_1, d_1} & x_{s_1, d_2} & x_{s_1, d_3} & \cdots & x_{s_1, d_J} \\x_{s_2, d_1} & x_{s_2, d_2} & x_{s_2, d_3} & \cdots & x_{s_2, d_J} \\x_{s_3, d_1} & x_{s_3, d_2} & x_{s_3, d_3} & \cdots & x_{s_3, d_J} \\\vdots & \vdots & \vdots & \ddots & \vdots \\x_{s_I, d_1} & x_{s_I, d_2} & x_{s_I, d_3} & \cdots & x_{s_I, d_J}\end{array}\right] \\&\end{aligned}$

式中: x_{si, dj}(i=1, 2, …, I; j=1, 2, …, J)是邻接矩阵A_SD的元素。

第3节给出考虑动态重构策略的装备体系可靠性定义及其模型, 并根据装备体系有效OODA网络模型给出有效OODA环及装备体系可靠性预计算法。

本文利用转移矩阵计算装备体系的有效OODA环数, 具体计算步骤如下。

步骤1    转移矩阵集合 A =[A_SD, A_DW]描述了装备体系异质有向图中从S类型节点到D类型节点, 以及从D类型节点到W类型节点的转移关系S→D→W。如果节点s_i, d_j, w_m存在, 且节点之间连通, 元素x_{si, dj}=x_{dj, wm}=1, 若节点之间不连通, 元素x_{si, dj}=x_{dj, wm}=0。可得x_{si, dj}, x_{dj, wm}的值为节点和连边示性函数的乘积, 如下所示:

(6) $\left\{\begin{array}{l}x_{s_i, d_j}=\alpha\left(s_i\right) \cdot \alpha\left(d_j\right) \cdot \alpha\left(e_{s_i, d_j}\right) \\x_{d_j, w_m}=\alpha\left(d_j\right) \cdot \alpha\left(w_n\right) \cdot \alpha\left(e_{d_j, w_m}\right)\end{array}\right.$

式中: α(·)表示每个节点和连边的存在性。

步骤2    节点S与W的邻接矩阵为A_SW: 相邻的转移矩阵A_SD和A_DW被定义为A_SD的到达节点类型与A_DW的起始节点类型相匹配的矩阵, 通过在相邻的转移矩阵相乘得到。A_SW提供了有向图从一种节点类型转换到另一种节点类型的概率信息, 可得OODA环数量为

(7) $N_{\mathrm{OODA}}=\sum\limits_{j=1}^J x_{s_i, d_j} \cdot x_{d_j, w_m}$

式中: N_OODA为装备体系中有效OODA环的数量; A_SD和A_DW的维数分别为I×J和J×M。进一步, t时刻装备体系的有效OODA环数量N_eOODA(t)计算如下。

每个矩阵元素的存在概率可以表示两个节点存在概率及其连边存在概率的乘积, 即:

(8) $\left\{\begin{array}{l}p\left(x_{s_i, d_j}\right)=p\left(s_i\right) \cdot p\left(d_j\right) \cdot p\left(e_{s_i, d_j}\right) \\p\left(x_{d_j, w_m}\right)=p\left(d_j\right) \cdot p\left(w_n\right) \cdot p\left(e_{d_j, w_m}\right)\end{array}\right.$

在节点失效和生成条件约束下, 各节点存在概率为

(9) $\left\{\begin{array}{l}p\left(s_i\right)=1-F_i^s\left(t_{\lambda_i^s}\right) \cdot G_i^s\left(t_{\mu_{i}^s}\right) \\p\left(d_j\right)=1-F_j^d\left(t_{\lambda_j^d}\right) \cdot G_j^d\left(t_{\mu_j^d}\right) \\p\left(w_m\right)=1-F_m^w\left(t_{\lambda_m^w}\right) \cdot G_m^w\left(t_{\mu_m^w}\right)\end{array}\right.$

若节点的失效或生成服从指数分布, 即有:

(10) $\left\{\begin{array}{l}p\left(s_i\right)=1-\exp \left(-\lambda_i^s \cdot t_{\lambda_i^s}\right) \cdot \exp \left(-\mu_i^s \cdot t_{\mu_i^s}\right) \\p\left(d_j\right)=1-\exp \left(-\lambda_j^d \cdot t_{\lambda_j^d}\right) \cdot \exp \left(-\mu_j^d \cdot t_{\mu_j^d}\right) \\p\left(w_m\right)=1-\exp \left(-\lambda_m^w \cdot t_{\lambda_m^w}\right) \cdot \exp \left(-\mu_m^w \cdot t_{\lambda_m^w}\right)\end{array}\right.$

若节点的失效或生成服从指数分布, 且考虑节点最大度攻击失效, 即有:

(11) $\left\{\begin{array}{l}p\left(s_i\right)=\left[1-\exp \left(-\lambda_i^s \cdot t_{\lambda_i^s}\right) \cdot \exp \left(-\mu_i^s \cdot t_{\mu_i^s}\right)\right] \cdot \alpha\left(k_i^s\right) \\p\left(d_j\right)=\left[1-\exp \left(-\lambda_j^d \cdot t_{\lambda_j^d}\right) \cdot \exp \left(-\mu_j^d \cdot t_{\mu_j^d}\right)\right] \cdot \alpha\left(k_j^d\right) \\p\left(w_m\right)=\left[1-\exp \left(-\lambda_m^w \cdot t_{\lambda_m^w}\right) \cdot \exp \left(-\mu_m^w \cdot t_{\lambda_m^w}\right)\right] \cdot \alpha\left(k_m^w\right)\end{array}\right.$

式中: F_i^s(t_λi^s), F_j^d(t_λj^d)和F_m^w(t_λm^w)分别表示自各节点上次修复以来时间的累积分布函数; G_i^s(t_μi^s), G_j^d(t_μj^d)和G_m^w(t_μm^w) 分别表示失效节点自故障以来时间的互补累积分布函数(complementary cumulative distribution function, CCDF); t_λi^s, t_λj^d和t_λm^w分别表示各节点上次修复后的时间; t_μi^s, t_μj^d和t_μm^w分别表示各节点上次故障后的时间; α(k_i^s), α(k_j^d)和α(k_m^w) 分别表示在最大度攻击下节点是否被移除的示性函数。

装备体系有效OODA环中通信链路的连通概率为

(12) $\left\{\begin{array}{l}p\left(e_{s_i, d_j}\right)=\alpha\left(\mathrm{cd}_{s_i, d_j}\right) \cdot R_{s_i, d_j}^c \\p\left(e_{d_j, w_m}\right)=\alpha\left(\operatorname{cd}_{d_j, w_m}\right) \cdot R_{d_j, w_m}^c\end{array}\right.$

式中: R_{si, dj}^c和R_{dj, wm}^c分别为通信系统可靠性, 由其分布函数计算得到; α(cd_{si, dj})和α(cd_{dj, wm})分别表示节点之间的距离在有效通信范围内, 由如下示性函数表示:

(13) $\alpha\left(d_{s_i, d_j}\right)=\left\{\begin{array}{l}1, \mathrm{~cd}_{s_i, d_j} \leqslant \min \left(\mathrm{cd}_{\text {max }}^{s_i}, \mathrm{~cd}_{\text {max }}^{d_j}\right) \\0, \mathrm{~cd}_{s_i, d_j}>\min \left(\mathrm{cd}_{\max }^{s_i}, \mathrm{~cd}_{\text {max }}^{d_j}\right)\end{array}\right.$

(14) $\alpha\left(d_{d_j, w_m}\right)=\left\{\begin{array}{l}1, \operatorname{cd}_{d_j, w_m} \leqslant \min \left(\mathrm{cd}_{\max }^{s_i}, \mathrm{~cd}_{\max }^{d_j}\right) \\0, \mathrm{~cd}_{d_j, w_m}>\min \left(\mathrm{cd}_{\max }^{d_j}, \mathrm{~cd}_{\max }^{w_{m}}\right)\end{array}\right.$

在第3.2节中, 将介绍装备体系的动态重构策略, 旨在提高装备体系在动态环境中的应变能力和任务可靠性。由于装备体系的资源共享与信息融合能力, 可通过装备体系耦合网络拓扑调控来抑制不同类型和强度的内外部扰动。动态重构策略可使装备体系能够根据不断变化的任务要求、资源可用性和环境条件动态调整其配置和行为。现阶段对装备体系耦合网络拓扑结构的防控策略研究主要关注防控策略和约束条件(经济和技术)等方面。资源层内所有感知与火力打击节点均围绕顶层任务进行多层决策, 因此一旦OODA环中的某个节点遭到破坏, 其重构机制能够快速反应, 立即组织其余功能相似节点进行重构, 从而构成新的OODA环, 继续执行任务。通过上述分析, 本文给出基于规则的装备体系重构策略, 如图 4所示。

重构策略Ⅰ: 簇内重构, 当簇内节点失效, 同一团簇内同类节点可进行协同重构, 该策略允许体系进行降级使用, 保持在任务基线之上。

重构策略Ⅱ: 簇间重构, 当团簇k内节点失效, 相邻团簇同类节点可通过中继节点进行协同, 该策略允许体系进行降级使用, 保持在任务基线之上。

重构策略Ⅲ: 当节点失效, 可通过修复或新增节点进行重构, 使体系恢复至完好状态, 但该策略需要消耗额外资源与费用。

有效OODA环考虑在节点和链路失效与动态重构条件下, 装备体系从侦察探测到火力毁伤的连续综合行动, 一个任务使命有多个OODA环耦合, 意味着有多种作战或者重构策略选择, 从而可提高装备体系整体效能和作战适用性。一个有效OODA环标志着一次有效作战任务的执行, OODA环的数量直接反映了装备体系作战能力的冗余程度, OODA环数越多, 冗余度越大, 体系的可靠性也就越高。因此, 本文选用装备体系中的OODA环数量作为衡量体系可靠性的指标。本文给出装备体系可靠性定义为装备体系在规定的条件下和规定的时间内, 完成规定任务的能力, 一般用R_SoS(t)表示。通过类比系统可靠性定义可知, 若装备体系内广义OODA环总数为N_OODA(0), 任务到t时刻广义OODA环发生断链数为r_OODA(t), 则装备体系在t时刻的可靠度观测值为

(15) $R_{\mathrm{SoS}}(t)=\frac{N_{\mathrm{OODA}}(0)-r_{\mathrm{OODA}}(t)}{N_{\mathrm{OODA}}(0)}$

本文定义N_eOODA(t)为装备体系在t时刻的有效广义OODA环数量, 即N_eOODA(t)=N_OODA(0)－r_OODA(t)。在体系可靠性概念定义中的OODA环可为广义作战环, 为既定装备体系组成要素(侦、控、打、引、防、保、评等)的作战或功能链条及其关联关系, 即装备体系形成作战能力的最小链路。

通过邻接矩阵和蒙特卡罗算法, 可以通过仿真得到装备体系的有效OODA环数和可靠度, N_sim为模拟次数。装备体系可靠性预计算法伪代码如算法1所示。

为了验证本文所提模型与算法的有效性, 以100个异构无人机构成的装备体系为研究对象进行案例应用研究。该装备体系具备侦察、指挥和火力打击等功能, 其中包含40个侦察类节点, 20个决策类节点, 40个火力节点, 通过高效协同为无人装备体系提供了强大的情报获取和打击能力。其他可靠性建模与预计所需参数如表 3所示。

首先, 在不考虑动态重构策略情况下对随机失效与蓄意攻击对装备体系的影响进行分析, 得到如图 5与图 6所示的装备体系有效OODA环数及可靠性变化情况。

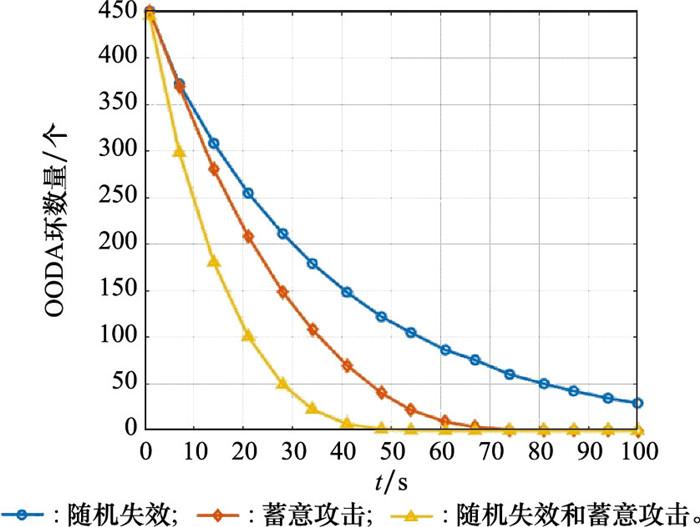
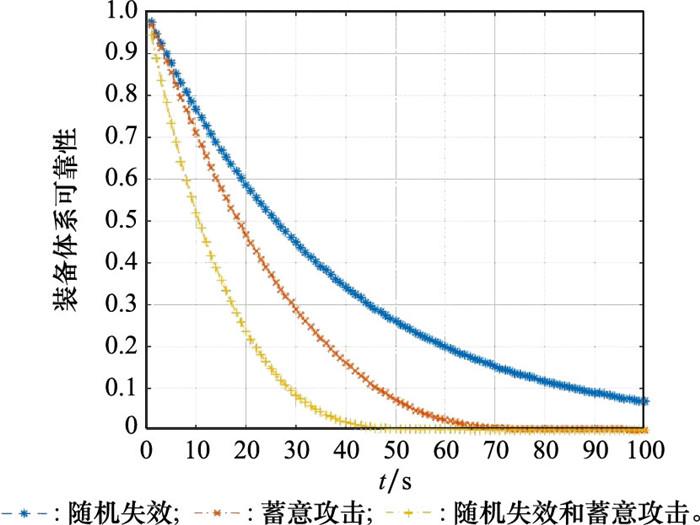
通过对比图 5与图 6可知, 在两种不同节点失效模式下, 无人装备体系的有效OODA环数会随着时间的推移而减少, 且两者在仿真初期下降趋势较快, 在仿真后期下降速度减缓。通过对随机失效和蓄意攻击策略进行比较可以看出, 蓄意攻击对装备体系影响效果较大, 因为蓄意攻击策略有选择地首先攻击装备体系中度最大的节点, 装备体系作战网络中会有更多的节点和链路被移除, 从而加速了装备体系OODA环数和可靠性的降低。当两类失效方式共同作用时, 装备体系作战网络中的OODA环数及装备体系可靠性在初期大幅度下降, 最终在仿真时间为45 s时降低至0, 比其他两类失效模型对装备体系的影响更大, 装备体系更容易被摧毁瓦解。

然后, 考虑随机失效和3种动态重构策略下, 对装备体系OODA环数及可靠性变化情况进行对比分析, 得到如图 7和图 8所示的有效OODA环的数量及装备体系可靠性。

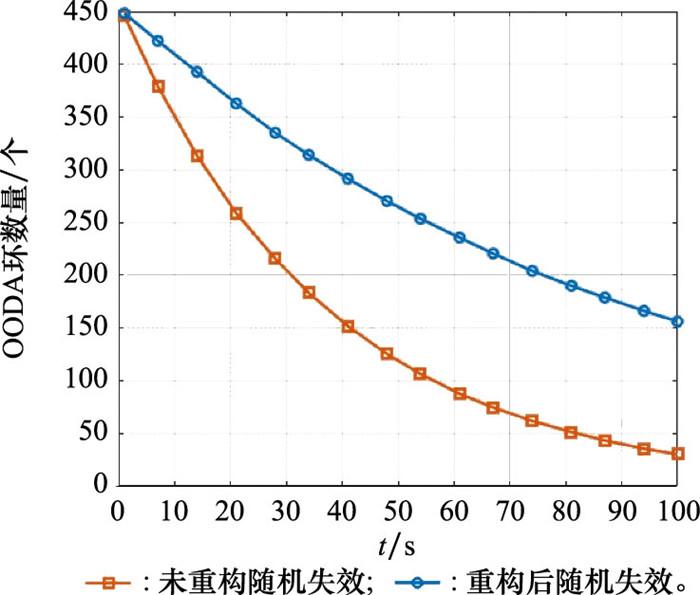
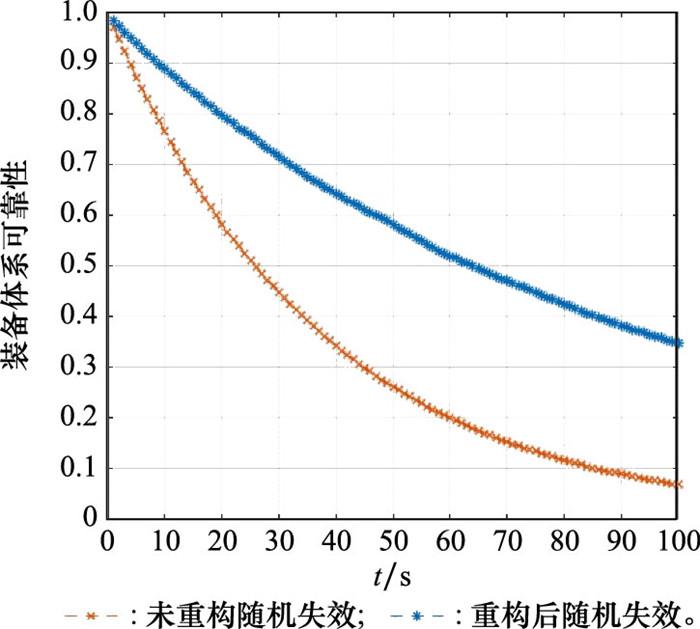
在考虑作战实体分配和物理资源约束的情况下, 基于动态重构策略的装备体系的OODA环的数量和可靠性在实际作战过程中随时间变化的趋势大致相同。随着重构策略Ⅰ、重构策略Ⅱ、重构策略Ⅲ的加入, 两者的变化都相对稳定, 呈现缓慢下降趋势。通过1 000次仿真模拟, 当t=100时, 有效OODA环的平均数量为156, 装备体系可靠性为0.357。未加入动态重构策略时, OODA环的平均数量为36, 装备体系可靠性为0.073。可见加入动态重构策略后, 无人装备体系有效OODA环数及可靠性有了较为明显的提升。

通过图 5和图 6可知, 当两类失效方式共同作用时对装备体系有效OODA环数及可靠性影响最大, 装备体系有效OODA环数量及可靠性都更迅速地下降为0。通过比较是否考虑动态重构策略, 对装备体系有效OODA环数及可靠性进行影响分析, 结果如图 9和图 10所示。

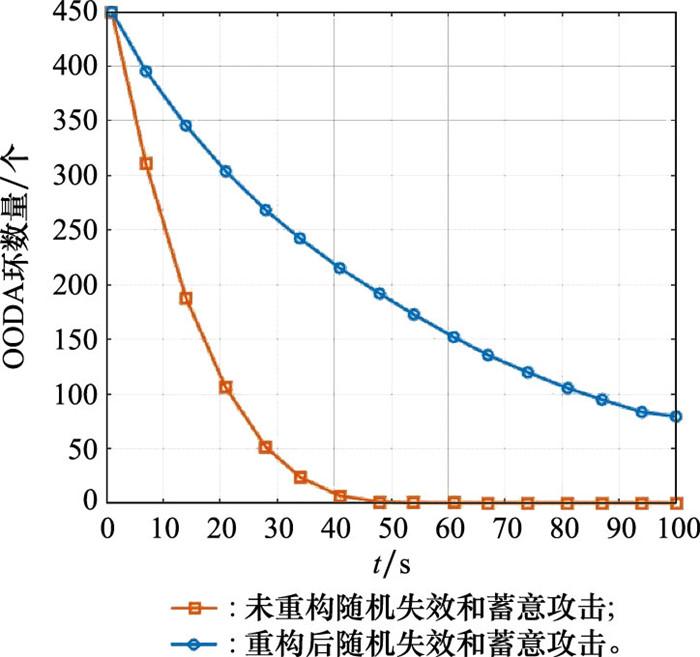
可以看出, 在考虑随机失效和蓄意攻击两种攻击模式共同作用的情况下, 考虑动态重构策略的装备体系有效OODA环数量和可靠性在实际作战过程中随时间的变化趋势大致相同。随着重构策略Ⅰ、重构策略Ⅱ、重构策略Ⅲ的加入, 两者变化相对稳定, 呈现缓慢下降趋势。通过仿真分析得出, 当t=100时, 有效OODA环平均数量为82, 装备体系可靠性为0.197, 而未考虑动态重构策略时有效OODA环数及装备体系可靠性均在仿真时间t=45时降为0。可见加入动态重构策略, 使装备体系有效OODA环数及可靠性产生较为明显的提升, 有效提高了装备体系的抗毁性及作战效能。

本文分析了装备体系可靠性相关概念内涵, 并提出了一种基于有效OODA环的装备体系可靠性建模与预计方法。首先, 给出了装备体系可靠性、维修性、测试性、保障性和安全性的概念内涵。其次, 根据装备体系的拓扑结构和要素, 建立其节点和链路模型, 并利用异质有向图提出了装备体系有效OODA环和OODA网络模型。然后, 考虑内外部干扰策略和动态重构策略, 创新性地建立了基于广义OODA环的装备体系可靠性建模与预计方法。最后, 以100个无人机构成的装备体系为例, 对可靠性建模与预计方法进行有效性和可行性验证。分析结果表明, 随着时间的推移, 装备体系有效OODA环数和可靠性逐渐下降, 且在初始阶段下降较快, 然后逐渐减缓; 其次, 内外部干扰失效对装备体系有效OODA环数和可靠性影响大于蓄意攻击失效和随机失效; 另外, 动态重构策略可有效提升装备体系在各种失效模式下的有效OODA环数和可靠性。本文研究可为装备体系可靠性定义、建模和预计提供理论与技术指导, 进而提升装备体系设计能力与作战效能。